题目内容
7.计算:(1)1-$\frac{3x}{2y}$÷$\frac{3x}{2y}$•$\frac{2y}{3x}$;
(2)$\frac{2(a-1)}{{a}^{2}+3a+2}$+$\frac{a}{{a}^{2}+2a+1}$-$\frac{3}{a+2}$.
分析 (1)先把除法变成乘法,再根据分式的乘法法则进行计算,最后算减法即可;
(2)先通分变成同分母的分式,再根据同分母的分式相加减法则进行计算,最后化成最简分式即可.
解答 解:(1)原式=1-$\frac{3x}{2y}$•$\frac{2y}{3x}$•$\frac{2y}{3x}$
=1-$\frac{2y}{3x}$
=$\frac{3x-2y}{3x}$;
(2)原式=$\frac{2(a-1)}{(a+1)(a+2)}$+$\frac{a}{(a+1)^{2}}$-$\frac{3}{a+2}$
=$\frac{2(a-1)(a+1)}{(a+1)^{2}(a+2)}$+$\frac{a(a+2)}{(a+1)^{2}(a+2)}$-$\frac{3(a+1)^{2}}{(a+1)^{2}(a+2)}$
=$\frac{-4a-5}{(a+1)^{2}(a+2)}$.
点评 本题考查了分式的混合运算的应用,能熟练地运用法则进行化简是解此题的关键.

练习册系列答案
相关题目
17.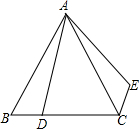 如图,△ABC是等边三角形,D为BC边上的点,△ABD绕点A沿逆时针方向旋转后到达△ACE的位置,那么旋转了( )
如图,△ABC是等边三角形,D为BC边上的点,△ABD绕点A沿逆时针方向旋转后到达△ACE的位置,那么旋转了( )
 如图,△ABC是等边三角形,D为BC边上的点,△ABD绕点A沿逆时针方向旋转后到达△ACE的位置,那么旋转了( )
如图,△ABC是等边三角形,D为BC边上的点,△ABD绕点A沿逆时针方向旋转后到达△ACE的位置,那么旋转了( )| A. | 75° | B. | 60° | C. | 45° | D. | 15° |
19.五边形的内角和的度数为( )
| A. | 180° | B. | 270° | C. | 360° | D. | 540° |
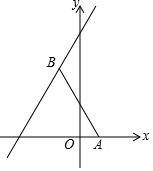 如图,点A的坐标为(2,0),点B在直线y=$\frac{4}{3}$x+4上运动,当线段AB最短时,AB的长度为4.
如图,点A的坐标为(2,0),点B在直线y=$\frac{4}{3}$x+4上运动,当线段AB最短时,AB的长度为4.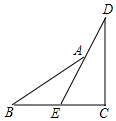 如图,阅读下面的题目及分析过程,并按要求进行证明.
如图,阅读下面的题目及分析过程,并按要求进行证明.