题目内容
15.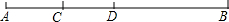 如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )
如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )| A. | 28 | B. | 29 | C. | 30 | D. | 31 |
分析 根据数轴和题意可知,所有线段的长度之和是AC+CD+DB+AD+CB+AB,然后根据CD=2,线段AB的长度是一个正整数,可以解答本题.
解答 解:由题意可得,
图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和是:AC+CD+DB+AD+CB+AB=(AC+CD+DB)+(AD+CB)+AB=AB+AB+CD+AB=3AB+CD,
∵CD=2,线段AB的长度是一个正整数,AB>CD,
∴当AB=8时,3AB+CD=3×8+2=26,
当AB=9时,3AB+CD=3×9+2=29,
当AB=10时,3AB+CD=3×10+2=32.
故选B.
点评 本题考查两点间的距离,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
6. a、b在数轴上位置如图所示,则|a-b|等于( )
a、b在数轴上位置如图所示,则|a-b|等于( )
 a、b在数轴上位置如图所示,则|a-b|等于( )
a、b在数轴上位置如图所示,则|a-b|等于( )| A. | -b-a | B. | a-b | C. | a+b | D. | -a+b |
3.计算2-(-3)×4的结果是( )
| A. | 20 | B. | -10 | C. | 14 | D. | -20 |
 如图,∠AOC=140°,OD平分∠AOC,OE平分∠BOC.
如图,∠AOC=140°,OD平分∠AOC,OE平分∠BOC.
 如图,在平面直角坐标系中,已知点A(0,8)、B(6,8)、C(6,0).点P同时满足下面两个条件:①P到∠AOC两边的距离相等;②PA=PB.
如图,在平面直角坐标系中,已知点A(0,8)、B(6,8)、C(6,0).点P同时满足下面两个条件:①P到∠AOC两边的距离相等;②PA=PB.