题目内容
5. 如图,∠AOC=140°,OD平分∠AOC,OE平分∠BOC.
如图,∠AOC=140°,OD平分∠AOC,OE平分∠BOC.(1)求∠BOE的度数.
(2)求∠DOE的度数.
分析 (1)根据邻补角的性质可得∠COB=180°-140°=40°,再根据角平分线的性质可得答案;
(2)由角平分线的定义可知$∠DOC=\frac{1}{2}∠AOC$=$\frac{1}{2}×140°$=70°,又∠COE=∠BOE=20°,∠DOE=∠DOC+∠COE,可得结果.
解答 解:(1)∵∠AOC=140°,
∴∠COB=180°-140°=40°,
∵OE平分∠BOC,
∴∠BOE=$\frac{1}{2}$∠BOC=20°;
(2)∵∠AOC=140°,OD平分∠AOC,
∴$∠DOC=\frac{1}{2}∠AOC$=$\frac{1}{2}×140°$=70°,
∵∠COE=∠BOE=20°,
∴∠DOE=∠DOC+∠COE=70°+20°=90°.
点评 本题主要考查了角平分线的定义,利用角平分线的定义计算角的度数是解答此题的关键.

练习册系列答案
相关题目
16. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.那么下列选项中,正确的是( )
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.那么下列选项中,正确的是( )
 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.那么下列选项中,正确的是( )
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.那么下列选项中,正确的是( )| A. | $\overrightarrow{OC}$=$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$) | B. | $\overrightarrow{OA}$=$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$) | C. | $\overrightarrow{OD}$=$\frac{1}{2}$($\overrightarrow{a}$-$\overrightarrow{b}$) | D. | $\overrightarrow{BD}$=($\overrightarrow{a}$-$\overrightarrow{b}$) |
13.若四边形ABCD的对角线交于点O,且有$\overrightarrow{AB}=2\overrightarrow{DC}$,则以下结论正确的是( )
| A. | $\overrightarrow{AO}=2\overrightarrow{OC}$ | B. | $|\overrightarrow{AC}|=|\overrightarrow{BD}|$ | C. | $\overrightarrow{AC}=\overrightarrow{BD}$ | D. | $\overrightarrow{DO}=2\overrightarrow{OB}$ |
14. 边长分别为a和2a的两个正方形按如图的样式摆放并连线,则图中阴影部分的面积为( )
边长分别为a和2a的两个正方形按如图的样式摆放并连线,则图中阴影部分的面积为( )
 边长分别为a和2a的两个正方形按如图的样式摆放并连线,则图中阴影部分的面积为( )
边长分别为a和2a的两个正方形按如图的样式摆放并连线,则图中阴影部分的面积为( )| A. | 3a2 | B. | $\frac{7}{4}{a}^{2}$ | C. | 2a2 | D. | $\frac{3}{2}{a}^{2}$ |
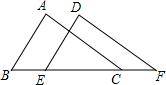 如图,在△ABC和△DEF,若AB=DE,BE=CF,要使△ABC≌△DEF,还需添加一个条件(只要写出一个就可以)是∠B=∠DEF.
如图,在△ABC和△DEF,若AB=DE,BE=CF,要使△ABC≌△DEF,还需添加一个条件(只要写出一个就可以)是∠B=∠DEF.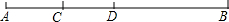 如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )
如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )