题目内容
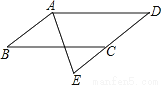
如图，四边形ABCD是平行四边形，AE平分∠BAD，交DC的延长线于点E．求证：DA=DE．
证明见解析.
【解析】试题分析：由平行四边形的性质得出AB∥CD，得出内错角相等∠E=∠BAE，再由角平分线证出∠E=∠DAE，即可得出结论．
试题解析：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠E=∠BAE，∵AE平分∠BAD，∴∠BAE=∠DAE，∴∠E=∠DAE，∴DA=DE．
练习册系列答案
阅读快车系列答案
相关题目
已知三角形的两边为3和4，则第三边a的取值范围是________．
1＜a＜7
【解析】根据三角形的三边关系：两边之和大于第三边，两边之差小于第三边，得4-3＜a＜4+3，即1＜a＜7．
故答案为：1＜a＜7． 如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．
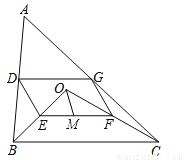
（1）求证：四边形DEFG是平行四边形；
（2）若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度．
（1）证明见解析；（2）6．
【解析】试题分析：（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC，DG∥BC且DG=BC，从而得到DE=EF，DG∥EF，再利用一组对边平行且相等的四边形是平行四边形证明即可；
（2）先判断出∠BOC=90°，再利用直角三角形斜边的中线等于斜边的一半，求出EF即可．
试题解析：（1）∵D、G分别是AB、AC的中点，... 如图，在?ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，若AB＝6，EF＝2，则BC的长为( )
A. 8 B. 10 C. 12 D. 14
B
【解析】试题分析：根据平行四边形的性质可知AB=CD，AD∥BC，AD=BC，然后根据平行线的性质和角平分线的性质可知AB=AF，DE=CD，因此可知AF+DE=AD+EF=2AB=12，解得AD=BC=12-2=10.
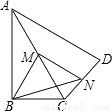
故选：B. 如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．
（1）求证：BM=MN；
（2）∠BAD=60°，AC平分∠BAD，AC=2，求BN的长．
（1）证明见解析；（2）
【解析】试题分析：（1）在△CAD中，由中位线定理得到MN∥AD，且MN=AD，在Rt△ABC中，因为M是AC的中点，故BM=AC，即可得到结论；
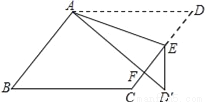
（2）由∠BAD=60°且AC平分∠BAD，得到∠BAC=∠DAC=30°，由（1）知，BM=AC=AM=MC，得到∠BMC =60°．由平行线性质得到∠NMC=∠DAC=30°，故∠BMN90°，得到，再由MN=... 如图，在?ABCD中，E为边CD上一点，将△ADE沿AE折叠至△AD′E处，AD′与CE交于点F．若∠B=52°，∠DAE=20°，则∠FED′的大小为________．
36°
【解析】试题分析：∵四边形ABCD是平行四边形，
∴∠D＝∠B＝52°，
由折叠的性质得：∠D′＝∠D＝52°，∠EAD′＝∠DAE＝20°，
∴∠AEF＝∠D＋∠DAE＝52°＋20°＝72°，∠AED′＝180°－∠EAD′－∠D′＝108°，
∴∠FED′＝108°－72°＝36°；
故答案为：36°． 如图，?ABCD的对角线AC，BD相交于点O，已知AD＝8，BD＝12，AC＝6，则△OBC的周长为( )
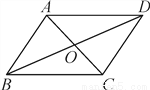
A. 13 B. 17 C. 20 D. 26
B
【解析】试题分析：由平行四边形的性质得出OA=OC=3，OB=OD=6，BC=AD=8，即可求出△OBC的周长．
【解析】
∵四边形ABCD是平行四边形，
∴OA=OC=3，OB=OD=6，BC=AD=8，
∴△OBC的周长=OB+OC+AD=3+6+8=17．
故选：B． 直线y=kx+b与抛物线y=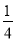
x2交于A（x1，y1）、B（x2，y2）两点，当OA⊥OB时，直线AB恒过一个定点，该定点坐标为_______________________．
（0，4）
【解析】【解析】
∵直线y=kx+b与抛物线y=x2交于A（x1，y1）、B（x2，y2）两点，∴kx+b=，
化简，得 x2﹣4kx﹣4b=0，∴x1+x2=4k，x1x2=﹣4b．
又∵OA⊥OB，∴ ，
解得，b=4，即直线y=kx+4，故直线恒过顶点（0，4）．
故答案为：（0，4）． 从标号分别为1，2，3，4，5的5张卡片中，随机抽取1张．下列事件中，必然事件是（ ）
A. 标号小于6 B. 标号大于6 C. 标号是奇数 D. 标号是3
A
【解析】试题分析：标号小于6是必然事件，标号大于6是不可能事件，标号是奇数是是随机事件，标号是3的事件是随机事件.
故选：A