��Ŀ����
��ͼ����?ABCD�У�EΪ��CD��һ�㣬����ADE��AE�۵�����AD��E����AD����CE���ڵ�F������B=52�㣬��DAE=20�㣬���FED��Ĵ�СΪ________��
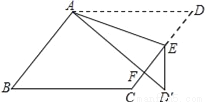
 36��
��������������������ı���ABCD��ƽ���ı��Σ�
���D����B��52�㣬
���۵������ʵã���D�䣽��D��52�㣬��EAD�䣽��DAE��20�㣬
���AEF����D����DAE��52�㣫20�㣽72�㣬��AED�䣽180�㣭��EAD�䣭��D�䣽108�㣬
���FED�䣽108�㣭72�㣽36�㣻
�ʴ�Ϊ��36�㣮
36��
��������������������ı���ABCD��ƽ���ı��Σ�
���D����B��52�㣬
���۵������ʵã���D�䣽��D��52�㣬��EAD�䣽��DAE��20�㣬
���AEF����D����DAE��52�㣫20�㣽72�㣬��AED�䣽180�㣭��EAD�䣭��D�䣽108�㣬
���FED�䣽108�㣭72�㣽36�㣻
�ʴ�Ϊ��36�㣮
 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д�����ʽ��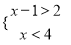 �Ľ⼯�ǣ�������
�Ľ⼯�ǣ�������
A. x��3 B. 3��x��4 C. x��4 D. ��
 B
���������ⲻ��ʽx��1��2���ã�x��3��
���ʽ��Ľ⼯Ϊ��3��x��4��
��ѡ��B��
B
���������ⲻ��ʽx��1��2���ã�x��3��
���ʽ��Ľ⼯Ϊ��3��x��4��
��ѡ��B�� ��ͼ���ڡ�ABC�У���D��E��F�ֱ��DZ�AB��BC��CA�ϵ��е㣬��AB=6cm��AC=8cm�����ı���ADEF���ܳ����� cm��
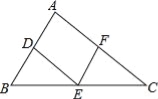
 14.
��������
�����������D��E�ֱ�AB��BC���е㣬��AD=AB��DE=AC.ͬ��AF=AC��EF=AB.��l�ı���ADEF=AD+DE+EF+AF=��AB+AC+AB+AC��=AB+AC=14cm.
14.
��������
�����������D��E�ֱ�AB��BC���е㣬��AD=AB��DE=AC.ͬ��AF=AC��EF=AB.��l�ı���ADEF=AD+DE+EF+AF=��AB+AC+AB+AC��=AB+AC=14cm. �����������У��ܹ��ж�һ���ı�����ƽ���ı��ε��ǣ�������
A. һ��Ա�ƽ�У���һ��Ա����
B. һ��Ա���ȣ�һ��Խ����
C. һ��Ա�ƽ�У�һ���Խ���ƽ����һ���Խ���
D. һ��Ա���ȣ�һ���Խ���ƽ����һ���Խ���
 C
��������A����������ı����п����ǵ������Σ�
B����������������ȫ�ȵ���������֤����ȵ�һ��Ա�ƽ�У�
C����ȷ����������������ȫ��֤��ƽ�е�һ��Ա���ȣ�����ƽ���ı��Σ�
D����������������ȫ�ȵ���������֤����ȵ�һ��Ա�ƽ�У�
��ѡC��
C
��������A����������ı����п����ǵ������Σ�
B����������������ȫ�ȵ���������֤����ȵ�һ��Ա�ƽ�У�
C����ȷ����������������ȫ��֤��ƽ�е�һ��Ա���ȣ�����ƽ���ı��Σ�
D����������������ȫ�ȵ���������֤����ȵ�һ��Ա�ƽ�У�
��ѡC�� ��ͼ���ı���ABCD��ƽ���ı��Σ�AEƽ�֡�BAD����DC���ӳ����ڵ�E����֤��DA=DE��
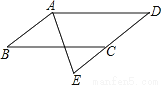
 ֤��������.
�������������������ƽ���ı��ε����ʵó�AB��CD���ó��ڴ�����ȡ�E=��BAE�����ɽ�ƽ����֤����E=��DAE�����ɵó����ۣ�
������������ı���ABCD��ƽ���ı��Σ���AB��CD�����E=��BAE����AEƽ�֡�BAD�����BAE=��DAE�����E=��DAE����DA=DE��
֤��������.
�������������������ƽ���ı��ε����ʵó�AB��CD���ó��ڴ�����ȡ�E=��BAE�����ɽ�ƽ����֤����E=��DAE�����ɵó����ۣ�
������������ı���ABCD��ƽ���ı��Σ���AB��CD�����E=��BAE����AEƽ�֡�BAD�����BAE=��DAE�����E=��DAE����DA=DE�� ��ͼ��DE�ǡ�ABC����λ�ߣ�����C��CF��BD��DE���ӳ����ڵ�F�������н�����ȷ���ǣ�������
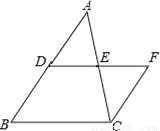
A. EF=CF B. EF=DE C. CF��BD D. EF��DE
 B
�������������������DE�ǡ�ABC����λ�ߣ�
��DE��BC��DE��BC��
��CF��BD��
���ı���BCFD��ƽ���ı��Σ�
��DF��BC��CF��BD��
��EF��DF��DE��BC��DE��BC��DE��
��ѡB��
B
�������������������DE�ǡ�ABC����λ�ߣ�
��DE��BC��DE��BC��
��CF��BD��
���ı���BCFD��ƽ���ı��Σ�
��DF��BC��CF��BD��
��EF��DF��DE��BC��DE��BC��DE��
��ѡB�� С��������һ��ƽ���ı��β����������ͼ���Ŀ飬Ϊ�������̵��䵽һ����ԭ����ͬ��ƽ���ı��β����������������鲣��������Ӧ���ǣ��� ����
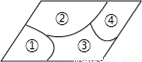
A. �٣��� B. �٣��� C. �ۣ��� D. �ڣ���
 D
�����������������⿼�����ƽ���ı��ε�����.
����������IJ����еĢں͢������ӵģ����Եõ��ı��εĴ�С.
��ѡB.
D
�����������������⿼�����ƽ���ı��ε�����.
����������IJ����еĢں͢������ӵģ����Եõ��ı��εĴ�С.
��ѡB. ������y=��x2+bx+c�ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���ʾ��
x | �� | ��2 | ��1 | 0 | 1 | 2 | �� |
y | �� | 0 | 4 | 6 | 6 | 4 | �� |
���ϱ���֪������˵���У�������ǣ� ��
A. ��������x���һ����������Ϊ����2��0��
B. ��������y��Ľ�������Ϊ��0��6��
C. �����ߵĶԳ�����ֱ��x=0
D. �������ڶԳ�����ಿ����������
 C
����������������
��x=��2ʱ��y=0���������߹�����2��0��������������x���һ����������Ϊ����2��0������A��ȷ��
��x=0ʱ��y=6������������y��Ľ�������Ϊ��0��6������B��ȷ��
��x=0��x=1ʱ��y=6����Գ���Ϊx=����C����
��x��ʱ��y��x������������������ڶԳ�����ಿ���������ģ���D��ȷ��
��ѡC��
C
����������������
��x=��2ʱ��y=0���������߹�����2��0��������������x���һ����������Ϊ����2��0������A��ȷ��
��x=0ʱ��y=6������������y��Ľ�������Ϊ��0��6������B��ȷ��
��x=0��x=1ʱ��y=6����Գ���Ϊx=����C����
��x��ʱ��y��x������������������ڶԳ�����ಿ���������ģ���D��ȷ��
��ѡC�� �����¼��У����ڱ�Ȼ�¼����ǣ�������
A. ���ӣ����ڲ��š����������� B. ����һ��Ӳ�����泯��
C. ������3������������һ���Ǻ��� D. ����һ������
 C
�����������������A�����ӣ����ڲ��š�����������������¼�����ΪҲ���ܲ����������ݣ�
B������һ��Ӳ�����泯��������¼���Ҳ���ܷ��泯�ϣ�
C. ������3������������һ���Ǻ����DZ�Ȼ�¼�����Ϊ������ֻ�к���������ô����ֻ����������
D������һ������������¼���Ҳ����ֻ���첻����.
��ѡC.
C
�����������������A�����ӣ����ڲ��š�����������������¼�����ΪҲ���ܲ����������ݣ�
B������һ��Ӳ�����泯��������¼���Ҳ���ܷ��泯�ϣ�
C. ������3������������һ���Ǻ����DZ�Ȼ�¼�����Ϊ������ֻ�к���������ô����ֻ����������
D������һ������������¼���Ҳ����ֻ���첻����.
��ѡC. 
