题目内容
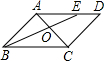
已知如图，∠A=90°，∠D=90°，且AE=DE，求证：∠ACB=∠DBC．
【答案】分析：由图片和已知，可得△ABE≌△DCE，则BE=CE，即可得到结论．
解答：证明：∵∠A=∠D=90°，AE=DE（已知），
∠AEB=∠DEC（对顶交相等），
∴△ABE≌△DCE（ASA），
∴BE=CE，
∴∠ACB=∠DBC．
点评：本题主要考查全等三角形全等的判定，还涉及到等腰三角形的性质知识点．
解答：证明：∵∠A=∠D=90°，AE=DE（已知），
∠AEB=∠DEC（对顶交相等），
∴△ABE≌△DCE（ASA），
∴BE=CE，
∴∠ACB=∠DBC．
点评：本题主要考查全等三角形全等的判定，还涉及到等腰三角形的性质知识点．
练习册系列答案
相关题目
19、已知如图，∠A=90°，∠D=90°，且AE=DE，求证：∠ACB=∠DBC．
