Question

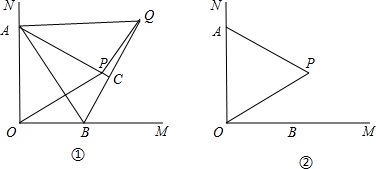
已知如图①，∠MON=90°，点A是射线ON上的一个定点，OA=4，点B是射线OM上的一个动点，分别以OA、AB为边在∠MON的内部作等边三角形AOP和ABQ，连接PQ
（1）求∠APQ的度数．
（2）当点B在射线OM上移动时，四边形AOPQ的形状也随之发生变化．它能变化成一个平行四边形吗？若能，确定点B的位置；若不能，说明理由．
（3）若直线AP与BQ相交于点C，设△ABQ的面积为S₁，四边形AOBP面积为S₂，当S₁=2S₂时，判定BQ与OB的位置关系．（可利用备用图）

Answer 1

分析：（1）关键等边三角形性质求出OA=AP，AB=AQ，∠OAP=∠BAQ=60°，推出∠OAB=∠QAC，证△APQ≌△AOB即可；
（2）根据OAP=60°∠APQ=90°，推出AO和PQ不平行即可判断答案；
（3）设OB=X，作PH⊥OM于H，根据面积公式求出S₁ S₂，即可求出答案．

解答：解：（1）∵等边△ABQ，△AOP，
∴OA=AP，AB=AQ，∠OAP=∠BAQ=60°，
∴∠OAB=∠QAC，
∴△APQ≌△AOB，
∴∠APQ=∠AOB=90°．

（2）不能是平行四边形，理由是：
∵∠OAP=60°∠APQ=90°，
∴∠OAP≠∠APQ，
∴AO与PQ不平行，
∴四边形AOPQ不可能成为平行四边形．

（3）设OB=X，作PH⊥OM于H，
∵AO=OP=AP=4，
∴∠POM=30°，PH=2；
S₂=S_△AOP+S_△OPB  

= 1 2 ×4×2 3 + 1 2 x×2=4 3 +x

AB2=16+x2，AB= 16+x2 ，AC= 3 2 16+x2

，
∴S1=

1

2

16+x2

•

3

2

16+x2

=

3

4

(16+x2)，
∴

3

4

(16+x2)=2(x+4

3)

，x=

8±16

2 3

=4

3

(∵x＞0)，
∴tan∠BAO=

3

，
∴∠BAO=60°，
∴AP与AB重合，BQ⊥OB．

点评：本题主要考查对等边三角形的性质，全等三角形的性质，平行四边形的性质，解直角三角形等知识点的理解和掌握，能综合运用性质进行推理是解此题的关键．