题目内容
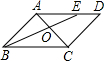
(任选做一题)(1)如图,在平行四边形ABCD中,E是AD上的一点.求证:AE•OB=OE•CB;
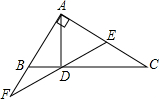
(2)已知如图,∠BAC=90°,AD⊥BC,AE=EC,ED延长线交AB的延长线于点F.
求证:①△DBF∽△ADF;②
| AB |
| AC |
| DF |
| AF |
分析:(1)根据平行四边形的性质可知AD∥BC,再根据平行线的性质及相似三角形的判定定理可得出△AOE∽△COB,再根据相似三角形的对应边成比例即可解答;
(2)①根据AD⊥BC,可知△ACD是直角三角形,再根据AE=CE可知DE是△ACD斜边的中线,故DE=CE,∠C=∠EDC,再根据对顶角相等可知∠BDF=∠C,再由直角三角形两锐角互余可知∠BAD=∠C,进而可求出△DBF∽△ADF;
②先求出Rt△ABD∽Rt△CAD,根据相似三角形的对应边成比例可知
=
,再由①中所求△DBF∽△ADF可知
=
,通过等量代换即可得出结论.
(2)①根据AD⊥BC,可知△ACD是直角三角形,再根据AE=CE可知DE是△ACD斜边的中线,故DE=CE,∠C=∠EDC,再根据对顶角相等可知∠BDF=∠C,再由直角三角形两锐角互余可知∠BAD=∠C,进而可求出△DBF∽△ADF;
②先求出Rt△ABD∽Rt△CAD,根据相似三角形的对应边成比例可知
| AB |
| AC |
| BD |
| AD |
| BD |
| AD |
| DF |
| AF |
解答:证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠EAO=∠ACB,∠AEO=∠EBC,
∴△AOE∽△COB,
∴
=
,即AE•OB=OE•CB;
(2)①∵AD⊥BC,
∴△ACD是直角三角形,
∵AE=CE,
∴DE是△ACD斜边的中线,
∴DE=CE,∠C=∠EDC,
∴∠BDF=∠C,
∵∠BAD+∠ABD=90°,∠C+∠ABD=90°,
∴∠BAD=∠C,
∵∠F=∠F,
∴△DBF∽△ADF;
②在Rt△ABD与Rt△CAD中,
∵∠BAD+∠ABD=90°,∠C+∠ABD=90°,
∴∠BAD=∠C,
∴Rt△ABD∽Rt△CAD,
∴
=
,
∵由①可知△DBF∽△ADF,
∴
=
,
∴
=
.
∴AD∥BC,∴∠EAO=∠ACB,∠AEO=∠EBC,
∴△AOE∽△COB,
∴
| AE |
| BC |
| OE |
| OB |
(2)①∵AD⊥BC,
∴△ACD是直角三角形,
∵AE=CE,
∴DE是△ACD斜边的中线,

∴DE=CE,∠C=∠EDC,
∴∠BDF=∠C,
∵∠BAD+∠ABD=90°,∠C+∠ABD=90°,
∴∠BAD=∠C,
∵∠F=∠F,
∴△DBF∽△ADF;
②在Rt△ABD与Rt△CAD中,
∵∠BAD+∠ABD=90°,∠C+∠ABD=90°,
∴∠BAD=∠C,
∴Rt△ABD∽Rt△CAD,
∴
| AB |
| AC |
| BD |
| AD |
∵由①可知△DBF∽△ADF,
∴
| BD |
| AD |
| DF |
| AF |
∴
| AB |
| AC |
| DF |
| AF |
点评:本题涉及到平行四边形的性质、相似三角形的判定与性质、直角三角形的性质,涉及面较广,但难易适中.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
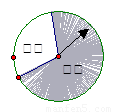
某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
(1)计算并完成表格:
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少(精确到1°)
|
转动转盘的次数n |
100 |
150 |
200 |
500 |
800 |
1000 |
|
落在“铅笔”的次数m |
68 |
111 |
136 |
345 |
564 |
701 |
|
落在“铅笔”的频率 |
|
|
|
|
|
|
(在下面的23、24两题中任选做一题,若两题都答,按23题评分)
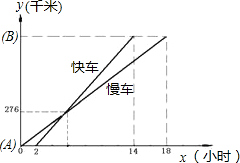 所示.请你根据图象,回答下列问题:
所示.请你根据图象,回答下列问题: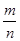

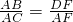 .
.

 .
.