题目内容
14.王华同学从A处沿北偏西60°方向走100m到B处,再从B处向正南方向走200m到C处,此时王华同学离A处的距离是173m.(结果保留整数,参考数据:$\sqrt{3}$≈1.732)分析 根据三角函数分别求AD,BD的长,从而得到CD的长.再利用勾股定理求AC的长即可.
解答 解:如图所示,在Rt△ADB中,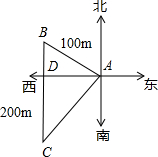
AD=AB•sin60°=50$\sqrt{3}$,BD=AB•cos60°=50,
∴CD=200-50=150,
∴Rt△ACD中,AC=$\sqrt{C{D}^{2}+A{D}^{2}}$=$\sqrt{15{0}^{2}+(50\sqrt{3})^{2}}$=100$\sqrt{3}$≈173,
即王华同学离A处的距离是173m.
故答案为:173.
点评 本题考查了解直角三角形--方向角问题.求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线,构造直角三角形.

练习册系列答案
相关题目
4.罗山西亚丽宝超市第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的$\frac{1}{2}$倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)
(1)罗山西亚丽宝超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品.其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
| 甲 | 乙 | |
| 进价(元/件) | 20 | 30 |
| 售价(元/件) | 29 | 40 |
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品.其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
14.三个连续奇数,中间一个是k,则这三个数的积为( )
| A. | k3-4k | B. | 8k3-8k | C. | 4k3-k | D. | 8k3-2k |
 在平面直角坐标系中,抛物线y=-x2+2bx+c与x轴交于点A、B(点A在点B的右侧),且与y轴正半轴交于点C,已知A(2,0)
在平面直角坐标系中,抛物线y=-x2+2bx+c与x轴交于点A、B(点A在点B的右侧),且与y轴正半轴交于点C,已知A(2,0)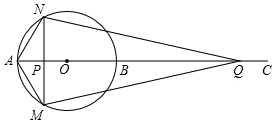 已知:如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为2,AC=10,设运动时间为ts.
已知:如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为2,AC=10,设运动时间为ts.