题目内容
19. 如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于E,若∠EAO=15°,则∠BOE的度数为( )
如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于E,若∠EAO=15°,则∠BOE的度数为( )| A. | 85° | B. | 80° | C. | 75° | D. | 70° |
分析 由矩形的性质得出OA=OB,再由角平分线得出△ABE是等腰直角三角形,得出AB=BE,证明△AOB是等边三角形,得出∠ABO=60°,OB=AB,得出OB=BE,由三角形内角和定理和等腰三角形的性质即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠EAO=15°,
∴∠BAO=45°+15°=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,OB=AB,
∴∠OBE=90-60°=30°,OB=BE,
∴∠BOE=$\frac{1}{2}$(180°-30°)=75°.
故选:C.
点评 本题考查了矩形的性质、等腰直角三角形的判定与性质、等边三角形的判定与性质、三角形内角和定理;熟练掌握矩形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11. 如图,若AB=AC,∠1=∠2,则下列条件不能使△ABD≌△ACE的是( )
如图,若AB=AC,∠1=∠2,则下列条件不能使△ABD≌△ACE的是( )
 如图,若AB=AC,∠1=∠2,则下列条件不能使△ABD≌△ACE的是( )
如图,若AB=AC,∠1=∠2,则下列条件不能使△ABD≌△ACE的是( )| A. | AE=AD | B. | ∠B=∠C | C. | ∠E=∠D | D. | BD=CE |
 利用平移求图中图形的周长.
利用平移求图中图形的周长.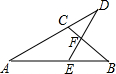 如图,在△ABC中,D是AC延长线上的一点,E是AB上的一点,连接DE交BC于点F,已知∠A=27°,∠EFB=85°,∠B=38°,求∠D和∠DEB的度数.
如图,在△ABC中,D是AC延长线上的一点,E是AB上的一点,连接DE交BC于点F,已知∠A=27°,∠EFB=85°,∠B=38°,求∠D和∠DEB的度数.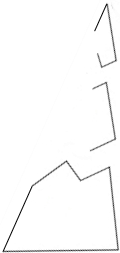 课外活动时,小明不小心将教室花架上的一块三角形玻璃打碎了,他看着地上的碎玻璃(如图)着急地说:“是我不小心打碎的.我想赶快去配一块,可玻璃已碎了,尺寸大小都不知道怎么办呢?”同学小灵说:“别急,只要你拿一块玻璃就可以去配上与原来完全相同的玻璃.”请想一想,应该拿哪一块呢?为什么?
课外活动时,小明不小心将教室花架上的一块三角形玻璃打碎了,他看着地上的碎玻璃(如图)着急地说:“是我不小心打碎的.我想赶快去配一块,可玻璃已碎了,尺寸大小都不知道怎么办呢?”同学小灵说:“别急,只要你拿一块玻璃就可以去配上与原来完全相同的玻璃.”请想一想,应该拿哪一块呢?为什么? 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G,请判断四边形GECF的形状,并证明你的结论.
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G,请判断四边形GECF的形状,并证明你的结论.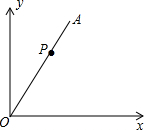 如图,P是∠AOx的边OA上的一点,且点P的坐标为(1,$\sqrt{3}$),则∠AOx=60度.
如图,P是∠AOx的边OA上的一点,且点P的坐标为(1,$\sqrt{3}$),则∠AOx=60度.