题目内容
10．
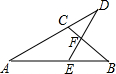如图，在△ABC中，D是AC延长线上的一点，E是AB上的一点，连接DE交BC于点F，已知∠A=27°，∠EFB=85°，∠B=38°，求∠D和∠DEB的度数．
分析 由三角形的外角性质求出∠AED，再由三角形内角和定理求出∠D，由邻补角关系求出∠DEB即可．
解答 解：∵∠EFB=85°，∠B=38°，
∴∠AED=∠EFB+∠B=85°+38°=123°，
∴∠D=180°-∠A-∠AED=180°-27°-123°=30°，
∠DEB=180°-∠AED=180°-123°=57°．
点评 本题考查了三角形的外角性质、三角形内角和定理；熟练掌握三角形的外角性质和三角形内角和定理，并能进行推理计算是解决问题的关键．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
如图，已知?ABCD中，∠AEF=∠ACB，AD=kAC，试判断AE、EF的数量关系．
2．
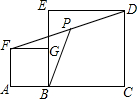如图，点A、B在一直线上，以AB、BC为边在同侧分别作正方形ABGF和正方形BCDE，点P是DF的中点，连结BP．已知AB=3cm，BC=9cm，则BP的值是（ ）
如图，点A、B在一直线上，以AB、BC为边在同侧分别作正方形ABGF和正方形BCDE，点P是DF的中点，连结BP．已知AB=3cm，BC=9cm，则BP的值是（ ）| A． | 6cm | B． | $\frac{3\sqrt{13}}{2}$cm | C． | 4$\sqrt{3}$cm | D． | 3$\sqrt{5}$cm |
19．
如图，在矩形ABCD中，AC、BD相交于点O，AE平分∠BAD交BC于E，若∠EAO=15°，则∠BOE的度数为（ ）
如图，在矩形ABCD中，AC、BD相交于点O，AE平分∠BAD交BC于E，若∠EAO=15°，则∠BOE的度数为（ ）| A． | 85° | B． | 80° | C． | 75° | D． | 70° |
