题目内容
18.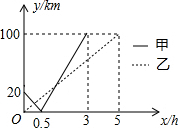 有甲、乙两军舰在南海执行任务.它们分别从A,B两处沿直线同时匀速前往C处,最终到达C处(A,B,C,三处顺次在同一直线上).设甲、乙两军舰行驶x(h)后,与B处相距的距离分别是y1(海里)和y2(海里),y1,y2与x的函数关系如图所示
有甲、乙两军舰在南海执行任务.它们分别从A,B两处沿直线同时匀速前往C处,最终到达C处(A,B,C,三处顺次在同一直线上).设甲、乙两军舰行驶x(h)后,与B处相距的距离分别是y1(海里)和y2(海里),y1,y2与x的函数关系如图所示(1)①在0≤x≤5的时间段内,y2与x之间的函数关系式为y2=20x(0≤x≤5).
②在0≤x≤0.5的时间段内,y1与x之间的函数关系式为y1=-40x+20(0≤x≤0.5)
(2)A,C两处之间的距离是120海里.
(3)若两军舰的距离不超过5海里是互相望到,当0.5≤x≤3时.求甲、乙两军舰可以互相望到时x的取值范围.
分析 (1)①设y2与x之间的函数关系式为y2=kx(0≤x≤5),将(5,100)代入,利用待定系数法求解;
②设y1与x之间的函数关系式为y1=mx+n(0≤x≤0.5),将(0,20),(0.5,0)代入,利用待定系数法求解;
(2)由于A,B,C,三处顺次在同一直线上,从图中可以看出A、B两处相距20km,B、C两处相距100km,则A、C两处之间的距离是为20+100=120海里;
(3)需要分类讨论:甲军舰追上乙军舰之前、后两种情况下,两军舰可以互相望到时x的取值范围.
解答 解:(1)①设y2与x之间的函数关系式为y2=kx(0≤x≤5),
将(5,100)代入,得100=5k,k=20,
所以y2与x之间的函数关系式为y2=20x(0≤x≤5);
②设y1与x之间的函数关系式为y1=mx+n(0≤x≤0.5),
将(0,20),(0.5,0)代入,
得$\left\{\begin{array}{l}{n=20}\\{0.5m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-40}\\{n=20}\end{array}\right.$,
所以y1与x之间的函数关系式为y1=-40x+20(0≤x≤0.5);
(2)A,C两处之间的距离是20+100=120海里;
(3)甲航速为20÷0.5=40(海里/h),
乙航速为100÷5=20(海里/h).
当甲军舰追上乙军舰之前两军舰的距离不超过5海里时,
(40-20)x≥20-5,
解得 x≥0.75.
当甲军舰追上乙军舰之后两军舰的距离不超过5海里时,
(40-20)x≤20+5,
解得,x≤1.25.
所以当0.5≤x≤3时,甲、乙两军舰可以互相望到时x的取值范围是0.75≤x≤1.25.
故答案为y2=20x(0≤x≤5);y1=-40x+20(0≤x≤0.5);120.
点评 本题考查了一次函数的应用,一次函数的图象,待定系数法求函数的解析式.利用数形结合、分类讨论是解题的关键.

 同步奥数系列答案
同步奥数系列答案| A. | 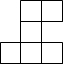 | B. | 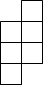 | C. | 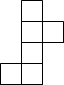 | D. |  |
| A. | $\sqrt{8}$-$\sqrt{3}$=$\sqrt{5}$ | B. | b2•b3=b6 | C. | 4a-9a=-5 | D. | (ab2)2=a2b4 |
 如图,立体图形的左视图是( )
如图,立体图形的左视图是( )| A. |  | B. |  | C. |  | D. |  |