题目内容
如图所示,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在BC边上,且∠GDF=∠ADF。
(1)求证:△ADE≌ABFE
(2)连接EG,判断EG与DF的位置关系,并说明理由。


(1)(4分)证明:∵AD∥BC,∴∠ADE=∠BFE,
∵E为AB的中点,∴AE=BE,
在△AED和△BFE中, ∠ADE=∠EFB, ∠AED=∠BEF, AE=BE
∴△AED≌△BFE(AAS);
(2)(4分)解 :EG与DF的位置关系是EG⊥DF,
:EG与DF的位置关系是EG⊥DF,
理由为:连接EG,

∵∠GDF=∠ADE,∠ADE=∠BFE, ∴∠GDF=∠BFE,
由(1)△AED≌△BFE得:DE=EF,即GE为DF上的中线,
∴GE垂直平分DF.

练习册系列答案
相关题目
 所在的平面直角坐标系中的纵轴(即y轴)向左平移1个单位,则原抛物线在新的坐标系下的函数关系式是______________.
所在的平面直角坐标系中的纵轴(即y轴)向左平移1个单位,则原抛物线在新的坐标系下的函数关系式是______________.

 的自变量x的取值范围在数轴上表示为
的自变量x的取值范围在数轴上表示为 ( )
( ) 
 的最简公分母是_ .
的最简公分母是_ . 与双曲线
与双曲线 交于
交于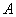 、
、 两
两 点,
点, 值;
值; 的不等式
的不等式 的解集;
的解集; 的纵坐标为8,求△
的纵坐标为8,求△ 的面积.
的面积.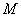 ,
, 轴上有点
轴上有点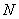 ,且点
,且点
 >b,则a+b= .
>b,则a+b= .