题目内容
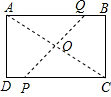
动手做一做：取一张长为12、宽为6的长方形纸片，然后将此纸片折叠起来，使相对的两个角的顶点重合．尝试用你所学过的数学知识求折痕的长．（要求：画出图形，并写出解题过程）
考点：翻折变换（折叠问题）
专题：应用题
分析：由长方形顶点A、C重合折叠可知，AC与PQ相互垂直平分，不妨设AC与PQ相交于点O，再证得△POC相似△ADC，进一步利用三角形相似的性质解答即可．
解答：解：由题意得，AD=6，AB=12，点A和点C折叠后重合，折痕为PQ，
如图，AC与PQ相交于点O，OC=
AC=
=3
，
∵顶点A、C重合，
∴AC与PQ相互垂直平分，
∴∠POC=90°，
而∠D=90°，∠OCP=∠DCA，
∴△POC∽△ADC，
∴
=
，
即PO=
=
，
得PO=
，
因此PQ=3
．
即折痕为3
．
如图，AC与PQ相交于点O，OC=
| 1 |
| 2 |
| 1 |
| 2 |
| AB2+BC2 |
| 5 |
∵顶点A、C重合，
∴AC与PQ相互垂直平分，
∴∠POC=90°，
而∠D=90°，∠OCP=∠DCA，
∴△POC∽△ADC，
∴
| PO |
| AD |
| OC |
| DC |
即PO=
| AD•OC |
| DC |
6×3
| ||
| 12 |
得PO=
3
| ||
| 2 |
因此PQ=3
| 5 |
即折痕为3
| 5 |
点评：此题考查了翻折变换的知识，解答本题主要利用矩形的性质，对称的性质以及三角形相似的判定与性质，有一定难度，解答时注意先画出示意图．
练习册系列答案
相关题目
小红帮助母亲预算家庭4月份电费开支情况，下表是小红家4月初连续8天每天早上电表显示的读数．若每度收电费0.5元，估计小红家4月份（按30天计）的电费是（ ）元．
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 电表显示度数 | 221 | 224 | 228 | 233 | 239 | 242 | 246 | 249 |
| A、114.75 | B、52.5 |
| C、60 | D、120 |
已知数串：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，…依照这前15个数的分子、分母的构成规律排列下去，第100个数是（ ）
| 1 |
| 1 |
| 2 |
| 1 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
| 5 |
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
| 4 |
| 1 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
方程组
（ ）
|
| A、无解 | B、有1组解 |
| C、有2组解 | D、有无穷多组解 |