题目内容
为了由数321321321321得到被9整除的最大的数，必须擦去的数码是 ，得到的被9整除的最大的数是 ．
考点：数的整除性
专题：计算题
分析：若一个整数的各个位数的数字和能被9整除，则这个整数能被9整除，为了使得到的数最大，从而可求出必须擦掉的数码．
解答：解：3+2+1+3+2+1+3+2+1+3+2+1=24，
所以必须减去6才能被9整除，
为了使最后得到的数最大，则必须使去掉的数字最少，且所去的数字在靠后的位置．
综上可得必须擦去数码3，去掉最后面的两个3，则得到的数为3213212121．
故答案为：3，3213212121．
所以必须减去6才能被9整除，
为了使最后得到的数最大，则必须使去掉的数字最少，且所去的数字在靠后的位置．
综上可得必须擦去数码3，去掉最后面的两个3，则得到的数为3213212121．
故答案为：3，3213212121．
点评：此题考查了数的整除性问题，解答本题的关键是掌握若一个整数的各个位数的数字和能被9整除，则这个整数能被9整除，有一定难度．
练习册系列答案
相关题目
如图，已知△ABC，图中的每个小正方形的边长为1；
．如图1，依次点击点A，C，
则计算机自动绘制出点C'．点C'是以点A为旋转中心，将点C按逆时针方向旋转90°以后得到的点．再依次点击点B，C，
，可得点C''．点C''是以点B为旋转中心，将点C按逆时针方向旋转90°以后得到的点．
，得到点D'；依次点击点B，D，
，得到点D''．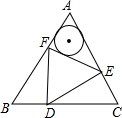
已知：如图，边长为a的正△ABC内有一边长为b的正△DEF，且a-b=2，则△AEF的内切圆半径为已知a，b均为非零有理数，5a与7b互为相反数，那么
=（ ）
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
信息处理：某市在全面建设小康社会的25项指标中，有16项完成了序时进度，其中10项已达到小康指标值．根据所给的数据和图表，完成下列各题：