题目内容
在直角三角中，∠C=90°，sinA与cosB的关系是 ．
考点：同角三角函数的关系
专题：
分析：利用锐角三角函数关系得出sinA=
，cosB=
，进而求出即可．
| BC |
| AB |
| AC |
| AB |
解答：
解：如图所示：∵sinA=
，cosB=
，
∴sin2A+cos2B=
+
=
=1．
故sinA与cosB的关系是：sin2A+cos2B=1．
故答案为：sin2A+cos2B=1．
解：如图所示：∵sinA=| BC |
| AB |
| AC |
| AB |
∴sin2A+cos2B=
| BC2 |
| AB2 |
| AC2 |
| AB2 |
| AB2 |
| AB2 |
故sinA与cosB的关系是：sin2A+cos2B=1．
故答案为：sin2A+cos2B=1．
点评：此题主要考查了同角三角函数的关系，正确记忆各锐角三角函数关系是解题关键．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
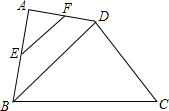在四边形ABCD中，BD是对角线，E，F分别是AB，AD的中点，若EF=2，tan∠DBC=
在△ABC和△ADE中，AC=AB，AE=AD，∠CAB=∠EAD=90°．