题目内容
△ABC的三边长比为3:5:6,与其相似的△A′B′C′的最长边为15厘米,且△ABC与△A′B′C′的相似比为
,则△ABC的最短边长为 .
| 2 |
| 3 |
考点:相似三角形的性质
专题:
分析:设△ABC的三边长分别为3x,5x,6x,再根据其相似的△A′B′C′的最长边为15厘米,且△ABC与△A′B′C′的相似比为
求出x的值,进而可得出结论.
| 2 |
| 3 |
解答:解:∵△ABC的三边长比为3:5:6,
∴设△ABC的三边长分别为3x,5x,6x,
∵与其相似的△A′B′C′的最长边为15厘米,且△ABC与△A′B′C′的相似比为
,
∴
=
,解得x=
,
∴3x=3×
=5(厘米).
故答案为:5厘米.
∴设△ABC的三边长分别为3x,5x,6x,
∵与其相似的△A′B′C′的最长边为15厘米,且△ABC与△A′B′C′的相似比为
| 2 |
| 3 |
∴
| 6x |
| 15 |
| 2 |
| 3 |
| 5 |
| 3 |
∴3x=3×
| 5 |
| 3 |
故答案为:5厘米.
点评:本题考查的是相似三角形的性质,熟知相似三角形的对应边的比叫相似比是解答此题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
下列说法正确的是( )
| A、若|a|=-a,则a<0 |
| B、若a<0,ab<0,则b>0 |
| C、式子3xy2-4x3y+12是七次三项式 |
| D、近似数1.4499保留一位小数约等于1.5 |
如果线段a,b,c,d满足ad=bc,则下列各式中不成立的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,若线段AB=20cm,点C是线段AB上一点,M、N分别是线段AC、BC的中点.
如图,若线段AB=20cm,点C是线段AB上一点,M、N分别是线段AC、BC的中点.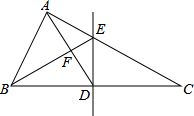 如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.