Question

如图，矩形ABCD中，AB=12cm，AD=16cm，动点E、F分别从A点、C点同时出发，均以2cm/s的速度分别沿AD向D点和沿CB向B点运动。

（1）经过几秒首次可使EF⊥AC？

（2）若EF⊥AC，在线段AC上，是否存在一点P，使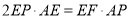？若存在，请说明P点的位置，并予以证明；若不存在，请说明理由。

Answer 1

（1）；（2）AP=．证明见解析.

【解析】

试题分析：（1）易证EF一定平分AC，当EF⊥AC时，△AEM∽△ACD，利用相似三角形的对应边的比相等即可求得AE的长，从而求得时间t的值；

（2）当EP⊥AD时，根据相似三角形的性质可以得到2EP•AE=EF•AP，根据△AEP∽△ADC，即可求得AP的长．

试题解析：（1）在直角△ACD中，AC=cm．

设经过ts时EF⊥AC．

则AE=CF=2t，

∵矩形ABCD中，AD∥BC，

∴∠DAC=∠ACF，

在△AME和△CMF中，

，

∴△AME≌△CMF（AAS）．

则AM=MC=AC=×20=10cm．

当EF⊥AC时，△AEM∽△ACD，

∴，

即 ，

解得：AE= ．

则t=（s）；

（2）存在．

∵△AME≌△CMF，

∴ME=MF=EF，

当EP⊥AD时，△AME∽△AEP，

，

即AE•EP=AP•ME=AP•EF，

即2EP•AE=EF•AP．

∵PE⊥AD，CD⊥AD，

∴EP∥CD，

∴△AEP∽△ADC，

∴，

即，

解得：AP=．

考点：相似形综合题．