题目内容
已知关于x的一元二次方程x2+2x+2k-1=0有两个不相等的实数根.
(1)求k的取值范围;
(2)当k=-1时,求方程的解.
(1)求k的取值范围;
(2)当k=-1时,求方程的解.
考点:根的判别式
专题:
分析:(1)根据一元二次方程的定义和△的意义得到△>0,即22-4(2k-1)>0,然后解不等式即可得到k的取值范围.
(2)把k=-1代入已知方程,然后利用因式分解法解方程.
(2)把k=-1代入已知方程,然后利用因式分解法解方程.
解答:解:(1)∵关于x的一元二次方程x2+2x+2k-1=0有两个不相等的实数根,
∴△>0,即22-4(2k-1)>0,
解得 k<1;
(2)把k=-1代入关于x的一元二次方程x2+2x+2k-1=0,得
x2+2x+2×(-1)-1=0,
整理,得
(x+3)(x-1)=0,
解得 x1=-3,x2=1.
∴△>0,即22-4(2k-1)>0,
解得 k<1;
(2)把k=-1代入关于x的一元二次方程x2+2x+2k-1=0,得
x2+2x+2×(-1)-1=0,
整理,得
(x+3)(x-1)=0,
解得 x1=-3,x2=1.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 如图,已知AB∥ED,∠CAB=135°,∠ACD=80°,求∠CDE的度数.
如图,已知AB∥ED,∠CAB=135°,∠ACD=80°,求∠CDE的度数.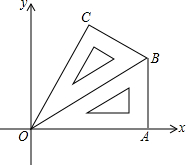 将一块三角板按如图所示放在直角坐标系中,∠OAB=90°,∠AOB=30°,AB=2.将三角板沿OB翻折后,得到△OBC.
将一块三角板按如图所示放在直角坐标系中,∠OAB=90°,∠AOB=30°,AB=2.将三角板沿OB翻折后,得到△OBC.