题目内容
15.关于x的一元二次方程x2-$\sqrt{2}$x+cosα=0有两个相等的实数根,则锐角a等于( )| A. | 0° | B. | 30° | C. | 45° | D. | 60° |
分析 根据方程的系数结合根的判别式即可得出关于cosα的一元一次方程,解之即可得出cosα的值,再根据特殊角的三角函数值即可得出锐角a的度数.
解答 解:∵关于x的一元二次方程x2-$\sqrt{2}$x+cosα=0有两个相等的实数根,
∴△=$(-\sqrt{2})^{2}$-4cosα=2-4cosα=0,
解得:cosα=$\frac{1}{2}$.
∵α为锐角,
∴α=60°.
故选D.
点评 本题考查了根的判别式以及特殊角的三角函数值,熟练掌握“当△=0时,方程有两个相等的实数根”是解题的关键.

练习册系列答案
相关题目
3.比2的相反数小的是( )
| A. | 5 | B. | -3 | C. | 0 | D. | -1 |
10.下列图形,是轴对称图形但不是中心对称图形的是( )
| A. | 正方形 | B. | 平行四边形 | C. | 等腰三角形 | D. | 圆 |
20.若(a+$\sqrt{2}$)2与|b+1-$\sqrt{2}$|互为相反数,则a+b的值为( )
| A. | -1 | B. | 1 | C. | 2$\sqrt{2}$-1 | D. | 2$\sqrt{2}$+1 |
19.下列计算正确的是( )
| A. | a4b-6a3b+9a2b=a2b(a2-6a+9) | B. | x2-2x+1=(x-1)2 | ||
| C. | x2-2x+4=(x-2)2 | D. | 4x2-y2=(4x+y)(4x-y) |
 ?ABCD的周长为20cm,AB<AD,对角线AC,BD相交于点O,OE⊥BD交AD于点E,则△ABE的周长为10cm.
?ABCD的周长为20cm,AB<AD,对角线AC,BD相交于点O,OE⊥BD交AD于点E,则△ABE的周长为10cm.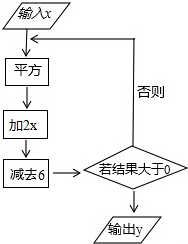 根据如图所示的程序计算:
根据如图所示的程序计算: