ЬтФПФкШн
дкЦНУцжБНЧзјБъЯЕ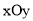 жаЃЌЖўДЮКЏЪ§
жаЃЌЖўДЮКЏЪ§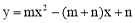 ЃЈ
ЃЈ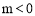 ЃЉЕФЭМЯѓгы
ЃЉЕФЭМЯѓгы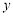 жсе§АыжсНЛгкAЕуЃЎ
жсе§АыжсНЛгкAЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃКИУЖўДЮКЏЪ§ЕФЭМЯѓгыxжсБигаСНИіНЛЕуЃЛ
ЃЈ2ЃЉЩшИУЖўДЮКЏЪ§ЕФЭМЯѓгыxжсЕФСНИіНЛЕужагвВрЕФНЛЕуЮЊЕуBЃЌШєЁЯABO=45ЁуЃЌНЋжБЯпABЯђЯТЦНвЦ2ИіЕЅЮЛЕУЕНжБЯпlЃЌЧѓжБЯпlЕФНтЮіЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЩшMЃЈpЃЌqЃЉЮЊЖўДЮКЏЪ§ЭМЯѓЩЯЕФвЛИіЖЏЕуЃЌЕБ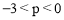 ЪБЃЌЕуMЙигкxжсЕФЖдГЦЕуЖМдкжБЯпlЕФЯТЗНЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ЪБЃЌЕуMЙигкxжсЕФЖдГЦЕуЖМдкжБЯпlЕФЯТЗНЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ

ЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉ ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЖўДЮКЏЪ§гывЛдЊЖўДЮЗНГЬЕФЙиЯЕЃЌвЊжЄУїЖўДЮКЏЪ§ЕФЭМЯѓгыxжсгаСНИіНЛЕуЃЌжЛвЊЖдгІЕФвЛдЊЖўДЮЗНГЬИљЕФХаБ№ЪНДѓгк0МДПЩ.
ЃЈ2ЃЉЧѓГіжБЯпABЕФНтЮіЪНЃЌИљОнЦНвЦЕФаджЪМДПЩЕУжБЯпlЕФНтЮіЪН.
ЃЈ3ЃЉЧѓГіЕуMЙигкxжсЕФЖдГЦЕу ЫљдкЕФЖўДЮКЏЪ§НтЮіЪНЃЌгЩЦфдкжБЯпlЕФЯТЗНЧѓГіmЕФШЁжЕЗЖЮЇЃЎ
ЫљдкЕФЖўДЮКЏЪ§НтЮіЪНЃЌгЩЦфдкжБЯпlЕФЯТЗНЧѓГіmЕФШЁжЕЗЖЮЇЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉСю ЃЌдђ
ЃЌдђ
 .
.
ЁпЖўДЮКЏЪ§ЭМЯѓгыyжсе§АыжсНЛгкAЕуЃЌ
Ёр ЃЌЧв
ЃЌЧв .
.
гж ЃЌЁр
ЃЌЁр .
.
Ёр .
.
ЁрИУЖўДЮКЏЪ§ЕФЭМЯѓгыxжсБигаСНИіНЛЕуЃЎ
ЃЈ2ЃЉСю ЃЌНтЕУЃК
ЃЌНтЕУЃК ЃЎ
ЃЎ
гЩЃЈ1ЃЉЕУ ЃЌЙЪBЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЎ
ЃЌЙЪBЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЎ
гжвђЮЊЁЯABO=45ЁуЃЌЫљвд ЃЌМД
ЃЌМД .
.
дђПЩЧѓЕУжБЯпABЕФНтЮіЪНЮЊ .
.
дйЯђЯТЦНвЦ2ИіЕЅЮЛПЩЕУЕНжБЯп ЃЎ
ЃЎ
ЃЈ3ЃЉгЩЃЈ2ЃЉЕУЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ
ЁпMЃЈpЃЌqЃЉЮЊЖўДЮКЏЪ§ЭМЯѓЩЯЕФвЛИіЖЏЕуЃЌ
Ёр .
.
ЁрЕуMЙигкxжсЕФЖдГЦЕу ЕФзјБъЮЊ
ЕФзјБъЮЊ .
.
ЁрЕу дкЖўДЮКЏЪ§
дкЖўДЮКЏЪ§ ЩЯ.
ЩЯ.
ЁпЕБ ЪБЃЌЕуMЙигкxжсЕФЖдГЦЕуЖМдкжБЯпlЕФЯТЗНЃЌ
ЪБЃЌЕуMЙигкxжсЕФЖдГЦЕуЖМдкжБЯпlЕФЯТЗНЃЌ
ЕБ ЪБЃЌ
ЪБЃЌ ЃЛЕБ
ЃЛЕБ ЪБЃЌ
ЪБЃЌ .
.
НсКЯЭМЯѓПЩжЊЃК ЃЌ
ЃЌ
НтЕУЃК .
.
Ёр ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ ЃЎ
ЃЎ

ПМЕуЃК1.ЖўДЮКЏЪ§злКЯЬтЃЛ2.ЦНвЦКЭжсЖдГЦЕФаджЪЃЛ3ЃЎЖўДЮКЏЪ§гывЛдЊЖўДЮЗНГЬЕФЙиЯЕЃЛ4ЃЎвЛдЊЖўДЮЗНГЬИљЕФХаБ№ЪН.

ФГЧјАЫФъМЖга3000УћбЇЩњВЮМгЁААЎЮвжаЛЊжЊЪЖОКШќЁБЛюЖЏЃЎЮЊСЫСЫНтБОДЮжЊЪЖОКШќЕФГЩМЈЗжВМЧщПіЃЌДгжаГщШЁСЫ200УћбЇЩњЕФЕУЗжНјааЭГМЦЃЎ
ЧыФуИљОнВЛЭъећЕФБэИёЃЌЛиД№ЯТСаЮЪЬтЃК
ГЩМЈxЃЈЗжЃЉ | ЦЕЪ§ | ЦЕТЪ |
50ЁмxЃМ60 | 10 | ____ |
60ЁмxЃМ70 | 16 | 0.08 |
70ЁмxЃМ80 | ____ | 0.20 |
80ЁмxЃМ90 | 62 | ____ |
90ЁмxЃМ100 | 72 | 0.36 |
ЃЈ1ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ

ЃЈ2ЃЉШєНЋЕУЗжзЊЛЏЮЊЕШМЖЃЌЙцЖЈ50ЁмxЃМ60ЦРЮЊЁАDЁБЃЌ60ЁмxЃМ70ЦРЮЊЁАCЁБЃЌ70ЁмxЃМ90ЦРЮЊЁАBЁБЃЌ90ЁмxЃМ100ЦРЮЊЁАAЁБЃЎетДЮШЋЧјАЫФъМЖВЮМгОКШќЕФбЇЩњдМгаЖрЩйбЇЩњВЮШќГЩМЈБЛЦРЮЊЁАDЁБЃП