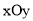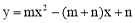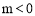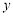Question

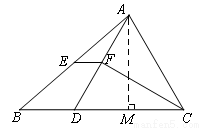
如图，△ABC中，BC >AC，点D在BC上，且CA=CD，∠ACB的平分线交AD于点F，E是AB的中点．

（1）求证：EF∥BD ；

（2）若∠ACB=60°，AC=8，BC=12，求四边形BDFE的面积．

 

 

Answer 1

（1）证明见解析；（2）.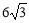

【解析】

试题分析：（1）由题意可推出△ADC为等腰三角形，CF为顶角的角平分线，所以也是底边上的中线和高，因此F为AD的中点，所以EF为△ABD的中位线，即EF∥BD.

（2）根据（1）的结论，可以推出△AEF∽△ABD，且S△AEF：S△ABD=1：4，所以S△AEF：S四边形BDEF=1：3，即可求出△AEF的面积，从而由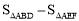求得四边形BDFE的面积．

（1）∵ CA=CD，CF平分∠ACB，∴ CF是AD边的中线．

∵ E是AB的中点，∴ EF是△ABD的中位线．

∴ EF∥BD .

（2）∵ ∠ACB=60°，CA=CD，∴ △CAD是等边三角形．

∴ ∠ADC=60°，AD=DC=AC=8．∴ BD=BC-CD=4．

如图，过点A作AM⊥BC，垂足为M ．

∴ ．．

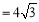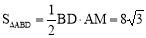∵ EF∥BD ，∴ △AEF ∽△ABD ，且．

∴ ．∴．

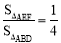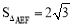四边形BDFE的面积=．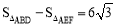

考点：1.等腰三角形的性质；2.三角形中位线定理；3.等边三角形的判定和性质；4.相似三角形的判定和性质；5.转换思想的应用．