题目内容
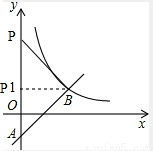
如图,在平面直角坐标系 中,一次函数
中,一次函数 (a为常数)的图象与y轴相交于点A,与函数
(a为常数)的图象与y轴相交于点A,与函数 的图象相交于点B
的图象相交于点B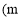 ,
, .
.
(1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请直接写出点P的坐标.

(1)(2,1),y=x-1;(2)(0,1)或(0,3).
【解析】
试题分析:(1)由点在函数图象上,得到点的坐标满足函数解析式,利用待定系数法即可求得.
(2)分两种情况,一种是∠BPA=90°,另一种是∠PBA=90°,所以有两种答案.
试题解析:(1)∵B在的图象上,
∴把B(m,1)代入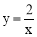 得m=2.
得m=2.
∴B点的坐标为(2,1).
∵B(2,1)在直线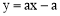 (a为常数)上,∴1=2a-a,∴a=1.
(a为常数)上,∴1=2a-a,∴a=1.
∴一次函数的解析式为y=x-1.
(2)如图,过B点向y轴作垂线交y轴于P点.此时∠BPA=90°.
∵B点的坐标为(2,1)∴P点的坐标为(0,1).
当PB⊥AB时,
在Rt△P1AB中,PB=2,PA=2,∴AB=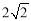 .
.
在等腰直角三角形PAB中,PB=PA=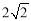 ,
,
∴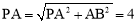 .∴OP=4-1=3.
.∴OP=4-1=3.
∴P点的坐标为(0,3).
∴P点的坐标为(0,1)或(0,3).
考点:1.反比例函数与一次函数的交点问题;2.分类思想的应用.

练习册系列答案
相关题目
下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 与方差
与方差 :
:
| 甲 | 乙 | 丙 | 丁 |
平均数 | 561 | 560 | 561 | 560 |
方差 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁




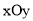
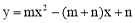
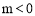
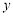
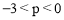





 ,并把解集在数轴上表示出来
,并把解集在数轴上表示出来