题目内容
16. 如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径.
如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径.(1)请你按以下步骤尺规作图:第一步,过点B作∠CBQ的角平分线交⊙O于点D;第二步,过D作PQ的垂线,垂足为E;
(2)求证:DE与⊙O相切;
(3)己知BC=10,BE=2,求DE的长.
分析 (1)利用尺规作图作出∠CBQ的角平分线和DE⊥PQ即可;
(2)连接OD,由OD=OB得出∠OBD=∠ODB,然后根据∠OBD=∠DBQ,得出∠ODB=∠DBQ,证得OD∥PQ,即可证得OD⊥DE,从而证得DE与⊙O相切;
(3)连接CD,根据圆周角定理证得∠BDC=90°,即可证得△BDC∽△BED,得出$\frac{BE}{BD}$=$\frac{BD}{BC}$,BD2=BE•BC=2×10=20,最后根据勾股定理即可求得DE的长.
解答 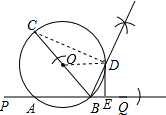 解:(1)如图:第一步,过点B作∠CBQ的角平分线交⊙O于点D;第二步,过D作PQ的垂线,垂足为E;
解:(1)如图:第一步,过点B作∠CBQ的角平分线交⊙O于点D;第二步,过D作PQ的垂线,垂足为E;
(2)连接OD,
∴OD=OB,
∴∠OBD=∠ODB,
∵∠OBD=∠DBQ,
∴∠ODB=∠DBQ,
∴OD∥PQ,
∵DE⊥PQ,
∴OD⊥DE,
∴DE与⊙O相切;
(3)连接CD,
∵BC是直径,
∴∠BDC=90°,
∵∠OBD=∠DBQ,∠BDC=∠DEB=90°,
∴△BDC∽△BED,
∴$\frac{BE}{BD}$=$\frac{BD}{BC}$,
∴BD2=BE•BC=2×10=20,
∴DE=$\sqrt{B{D}^{2}-B{E}^{2}}$=$\sqrt{20-{2}^{2}}$=4.
点评 本题考查了尺规作图,切线的判定,圆周角定理,三角形相似的判定和性质,勾股定理的应用等,作出辅助线构建等腰三角形和直角三角形是解题的关键.

练习册系列答案
相关题目
6.下列方程是一元二次方程的是( )
| A. | 2x2-7=3y+1 | B. | 5x2+$\frac{1}{x}$+4=0 | C. | $\frac{\sqrt{7}}{3}$x-$\sqrt{5}$=$\frac{{x}^{2}}{2}$+x | D. | ax2+bx+c=0 |
11.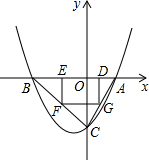 如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
(1)求抛物线表达式及A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并求出面积的最大值及m的取值范围.
 如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:| x | … | -3 | -2 | 1 | 2 | … |
| y | … | $-\frac{5}{2}$ | -4 | $-\frac{5}{2}$ | 0 | … |
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并求出面积的最大值及m的取值范围.
6.若方程组$\left\{\begin{array}{l}{x-2y=3}\\{3x+4y=5}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2.2}\\{y=-0.4}\end{array}\right.$,则方程组$\left\{\begin{array}{l}{(a+2012)-2(b-2013)=3}\\{3(a+2012)+4(b-2013)=5}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{a=2.2}\\{b=-0.4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=2014.2}\\{b=2012.6}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{a=-2009.8}\\{b=2012.6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=2014.2}\\{b=2013.4}\end{array}\right.$ |

 如图,在Rt△ABC中,AC=4,BC=6,在其内部做一个矩形CDEF,其中CD和CF分别在两条直角边上.
如图,在Rt△ABC中,AC=4,BC=6,在其内部做一个矩形CDEF,其中CD和CF分别在两条直角边上.