题目内容
已知y=ax2-2x+1与x轴没有交点,那么该抛物线的顶点在第( )象限.
| A、一 | B、二 | C、三 | D、四 |
考点:抛物线与x轴的交点
专题:
分析:首先根据题意得出b2-4ac=4-4a<0,进而得出对称轴的位置,结合图象开口方向得出抛物线的顶点的位置.
解答:解:∵y=ax2-2x+1与x轴没有交点,
∴b2-4ac=4-4a<0,
解得:a>1,
∴抛物线的开口方向向上,
∵a>1,b=-2,
∴对称轴在y轴的右侧,
故该抛物线的顶点在第一象限.
故选:A.
∴b2-4ac=4-4a<0,
解得:a>1,
∴抛物线的开口方向向上,
∵a>1,b=-2,
∴对称轴在y轴的右侧,
故该抛物线的顶点在第一象限.
故选:A.
点评:此题主要考查了抛物线与x轴的交点,得出对称轴位置是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
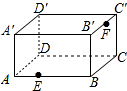 如图是放在地面上的一个长方体盒子,其中AB=9,BB′=5,B′C′=6,在线段AB的三等分点E(靠近点A)处有一只蚂蚁,B′C′中点F处有一米粒,则蚂蚁沿长方体表面爬到米粒处的最短距离为( )
如图是放在地面上的一个长方体盒子,其中AB=9,BB′=5,B′C′=6,在线段AB的三等分点E(靠近点A)处有一只蚂蚁,B′C′中点F处有一米粒,则蚂蚁沿长方体表面爬到米粒处的最短距离为( )| A、10 | ||
B、
| ||
C、5+3
| ||
D、6+
|
在△ABC中,∠B的平分线与∠C的平分线相交于O,且∠BOC=130°,则∠A=( )
| A、50° | B、60° |
| C、80° | D、100° |
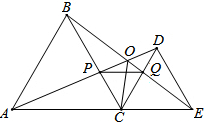 如图,△ABC、△CDE都是等边三角形,且点A、C、E在一条直线上,AD与BE、AD与BC、BE与CD分别交于点O、点P、点Q.求证:
如图,△ABC、△CDE都是等边三角形,且点A、C、E在一条直线上,AD与BE、AD与BC、BE与CD分别交于点O、点P、点Q.求证: 如图,AD⊥AB,AD=AB,CE=CD,BE⊥BD,试判断线段CD和线段CE的位置关系,并证明.
如图,AD⊥AB,AD=AB,CE=CD,BE⊥BD,试判断线段CD和线段CE的位置关系,并证明.