题目内容
11.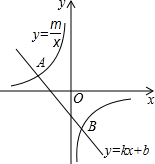 已知A(-3,2)、B(n,-3)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点.
已知A(-3,2)、B(n,-3)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点.(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
分析 (1)首先把A的坐标代入反比例函数解析式,求得反比例函数解析式,然后把B代入反比例函数解析式求得B的坐标,再根据待定系数法求得一次函数解析式;
(2)一次函数的值小于反比例函数的值的x的取值范围,就是一次函数的图象在反比例函数的图象的下边部分自变量x的范围.
解答 解:(1)把(-3,2)代入y=$\frac{m}{x}$得m=-6,
则反比例函数的解析式是y=-$\frac{6}{x}$.
把(n,-3)代入y=-$\frac{6}{x}$得n=2,
则B的坐标是(2,-3).
根据题意得$\left\{\begin{array}{l}{-3k+b=2}\\{2k+b=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$,
则反比例函数的解析式是y=-x-1;
(2)根据图象可得x的取值范围是-3<x<0或x>2.
点评 本题考查了用待定系数法求出一次函数、反比例函数的解析式,一次函数与反比例函数的交点问题的应用,主要考查学生能否运用这些性质进行计算,本题具有一定的代表性,是一道不错的题目,数形结合思想的运用.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
16.下列命题正确的是( )
①三角形中最大内角一定不小于60°; ②所有等腰直角三角形都相似;
③正多边形的外角为24°,则它的中心角也为24°; ④顺次连接对角线相等的四边形各边中点得到矩形.
①三角形中最大内角一定不小于60°; ②所有等腰直角三角形都相似;
③正多边形的外角为24°,则它的中心角也为24°; ④顺次连接对角线相等的四边形各边中点得到矩形.
| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ①②④ |
1.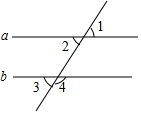 如图,根据下列条件不可以判定a∥b的是( )
如图,根据下列条件不可以判定a∥b的是( )
 如图,根据下列条件不可以判定a∥b的是( )
如图,根据下列条件不可以判定a∥b的是( )| A. | ∠2=∠3 | B. | ∠1=∠3 | C. | ∠1=∠4 | D. | ∠1+∠4=180° |
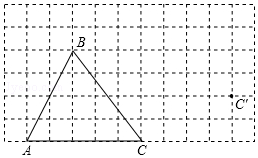 画图并填空:
画图并填空: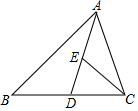 如图,AD为△ABC中的中线,E为AD中点,且△AEC的面积为3,则△ABC的面积为12.
如图,AD为△ABC中的中线,E为AD中点,且△AEC的面积为3,则△ABC的面积为12.