题目内容
10.阅读材料:若m2-2mn+2n2-8n+16=0,求m、n的值.解:∵m2-2mn+2n2-8n+16=0,
∴(m2-2mn+n2)+(n2-8n+16)=0,∴(m-n)2+(n-4)2=0,
∴(m-n)2=0,(n-4)2=0,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)已知x2+2xy+2y2+4y+4=0,求2x+y的值;
(2)已知△ABC的三边长a、b、c,且满足a2+b2-6a-8b+25=0,求△ABC的最大边c的范围;
(3)已知a-b=4,ab+c2-6c+13=0,则a+b+c=3.
分析 (1)配方得:(x+y)2+(y+2)2=0,再利用非负性列式可求得x、y的值,代入求结论;
(2)配方得:(a-3)2+(b-4)2=0,再利用非负性列式可求得a、b的值,根据三角形三边关系求△ABC的最大边c的范围;
(3)将a=b+4代入ab+c2-6c+13=0中,配方可求出b、c的值,再求a的值,代入即可.
解答 解:(1)x2+2xy+2y2+4y+4=0,
x2+2xy+y2+y2+4y+4=0,
(x+y)2+(y+2)2=0,
∴(x+y)2=0,(y+2)2=0,
∴x=2,y=-2;
∴2x+y=2×2-2=2;
(2)a2+b2-6a-8b+25=0,
a2-6a+9+b2-8b+16=0
(a-3)2+(b-4)2=0
∴(a-3)2=0,(b-4)2=0,
∴a=3,b=4;
∴4-3<c<4+3,
∴1<c<7,
∵c是最大边,
∴4≤c<7,
答:△ABC的最大边c的范围是:4≤c<7;
(3)∵a-b=4,
∴a=b+4,
代入得:b(b+4)+c2-6c+13=0,
b2+4b+4+c2-6c+9=0,
(b+2)2+(c-3)2=0,
∴b=-2,c=3,
∴a=b+4=-2+4=2,
∴a+b+c=2-2+3=3;
故答案为:3.
点评 本题是阅读材料问题,考查了完全平方式、非负性、三角形的三边关系,属于常考题型,本题的关键是完全平方公式要熟练掌握,明确三角形的两边之和大于第三边,两边之差小于第三边.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
11.已知关于x、y的二元一次方程组$\left\{\begin{array}{l}{x+2y=3}\\{3x+5y=m+2}\end{array}\right.$的解满足x+y=0,求有理数m的值.
18.已知方程x2+kx+6=0的两个根比方程x2-kx+6=0的两个根都大5,那么k的值是( )
| A. | -5 | B. | 5 | C. | 0 | D. | 1 |
20.下列计算正确的是( )
| A. | 3a+b=3ab | B. | -a2b+2a2b=a2b | C. | 2a3+3a2=5a3 | D. | 3a-a=2 |
 把如图所示的图形分成4个全等的图形.
把如图所示的图形分成4个全等的图形.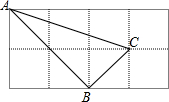 如图,在2×4的方格纸中,△ABC的3个顶点都在小正方形的顶点,这叫做格点三角形.则作出另一个格点三角形DEF,使△DEF≌△ABC,这样的三角形共有7个.
如图,在2×4的方格纸中,△ABC的3个顶点都在小正方形的顶点,这叫做格点三角形.则作出另一个格点三角形DEF,使△DEF≌△ABC,这样的三角形共有7个.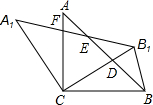 如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F
如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F