Question

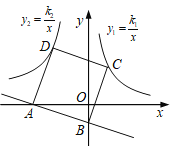
【题目】如图，抛物线过原点，且与轴交于点．

（1）求抛物线的解析式及顶点的坐标；

（2）已知为抛物线上一点，连接，，，求的值；

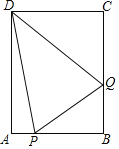
（3）在第一象限的抛物线上是否存在一点，过点作轴于点，使以，，三点为顶点的三角形与相似，若存在，求出满足条件的点的坐标；若不存在，请说明理由．

Answer 1

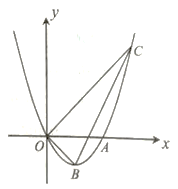
【答案】（1）抛物线的解析式为；顶点的坐标为；（2）3；（3）点的坐标为或．

【解析】

（1）用待定系数法即可求出抛物线的解析式，进而即可求出顶点坐标；

（2）先将点C的横坐标代入抛物线的解析式中求出纵坐标，根据B,C的坐标得出，，从而有，最后利用求解即可；

（3）设为．由于，所以当以，，三点为顶点的三角形与相似时，分两种情况：或，分别建立方程计算即可．

解：（1）∵抛物线过原点，且与轴交于点，

∴，解得．

∴抛物线的解析式为．

∵，

∴顶点的坐标为．

（2）∵在抛物线上，

∴．

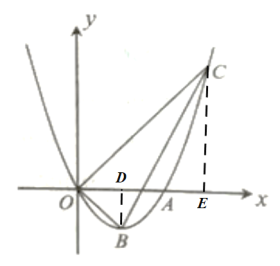
作轴于，作轴于，

则，，

∴，．

∴．

∵，．

∴．

（3）假设存在．

设点的横坐标为，则为．

由于，

所以当以，，三点为顶点的三角形与相似时，

有或

∴ 或．

解得或．

∴存在点，使以，，三点为顶点的三角形与相似．

∴点的坐标为或．