题目内容
20．
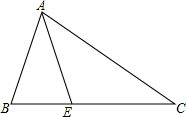如图，在△ABC中，AC=BC，∠C=36°，AE平分∠BAC，若AB=2，则AC=$\sqrt{5}$+1．
分析 根据等腰三角形的性质求出∠BAE的度数，证明△CAB∽△ABE，根据相似三角形的性质得到比例式，代入计算即可．
解答 解：∵AC=BC，∠C=36°，
∴∠BAC=∠B=72°，
∵AE平分∠BAC，
∴∠BAE=∠EAC=36°，
∴AB=AE=EC，
∴△CAB∽△ABE，
∴$\frac{AB}{BE}$=$\frac{AC}{AB}$，即AB2=AC•BE，
∴AB2=AC2-AC•AB，
解得AC=$\sqrt{5}$+1．
故答案为：$\sqrt{5}$+1．
点评 本题考查的是等腰三角形的性质、相似三角形的判定和性质，根据题意证明点E是线段BC的黄金分割点是解题的关键．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
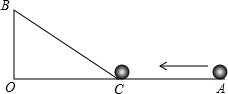如图，∠AOB=90°，OA=36cm，OB=12cm，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少？
某校有一块边长为a的正方形花圃．它有两横一纵宽度均为b的3条人行道（如图）把花圃分隔成6块，该花圃的实际种花面积是多少？