题目内容

9．若已知（x-3）5=a1x5+a2x4+a3x3+a4x2+a5x+a6
当x=2时，25a1+24a2+23a3+22a4+2a5+a6=-1；
当x=4时，45a1+44a2+43a3+42a4+4a5+a6=1．
（1）求a1+a2+a3+a4+a5+a6的值
（2）求a6的值．

分析 （1）将x=1代入可求得a1+a2+a3+a4+a5+a6的值；
（2）将x=0代入可求得a6的值．

解答 解：（1）将x=1代入得：原式=a1+a2+a3+a4+a5+a6=（1-3）5=-32；
（2）将x=0代入得：原式=a6=（0-3）5=-243．

点评 本题主要考查的是求代数式的值，代入特殊数值是解题的关键．

练习册系列答案
相关题目
19．下列几种说法正确的是（　　）
A．-a一定是负数B．|a|一定是正数
C．平方后等于9的数是3D．0的相反数是0
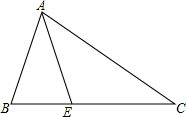20．如图，在△ABC中，AC=BC，∠C=36°，AE平分∠BAC，若AB=2，则AC=$\sqrt{5}$+1．
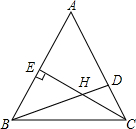17．在Rt△ABC中，∠C=90°，a，b分别为∠A，∠B的对边，若b=3，tanA=$\frac{3}{4}$，则a=$\frac{9}{4}$．
4．△ABC中，∠A：∠ABC：∠ACB=3：4：5，CE是AB上的高，∠BHC=135°，求证：BD⊥AC．
14．若$\sqrt{a-3}$+（b+2）2=0，则a+b=1．
1．已知等式ax+c=ay+c，则下列等式不一定成立的是（　　）
A．ax=ayB．x=yC．m-ax=m-ayD．2ax=2ay
18．如果等式$\frac{a+2}{-2}$=1-b成立，则a+2=2b-2，这是根据等式的性质2在等式中的运用．
19．计算（0.09）${\;}^{-\frac{1}{2}}$-（2$\frac{7}{9}$）${\;}^{\frac{1}{2}}$-（4$\frac{17}{27}$）${\;}^{-\frac{1}{3}}$+（$\frac{5}{9}$）-1-729${\;}^{-\frac{1}{6}}$=$\frac{38}{15}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网