题目内容
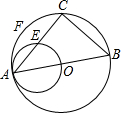 如图,已知△ABC内接于⊙O,AB为⊙O的直径,AB=8cm,以OA为直径的⊙D与⊙O的弦AC交于E点,若CE=2cm,求:
如图,已知△ABC内接于⊙O,AB为⊙O的直径,AB=8cm,以OA为直径的⊙D与⊙O的弦AC交于E点,若CE=2cm,求:(1)AC的长;
(2)
 |
| AC |
考点:圆周角定理,垂径定理
专题:计算题
分析:(1)连结OE,如图,根据圆周角定理得∠AEO=90°,则OE⊥AC,然后根据垂径定理得到AE=CE=2,则AC=4;
(2)根据圆周角定理由AB为⊙O的直径得到∠ACB=90°,由于AB=8,AC=4,根据含30度的直角三角形三边的关系得到∠B=30°.
(2)根据圆周角定理由AB为⊙O的直径得到∠ACB=90°,由于AB=8,AC=4,根据含30度的直角三角形三边的关系得到∠B=30°.
解答:解: (1)连结OE,如图,
(1)连结OE,如图,
∵OA为⊙D的直径,
∴∠AEO=90°,
∴OE⊥AC,
∴AE=CE=2,
∴AC=4;
(2)∵AB为⊙O的直径,
∴∠ACB=90°,
∵AB=8,AC=4,
即AC=
AB,
∴∠B=30°,
即
所对的圆周角为30°.
 (1)连结OE,如图,
(1)连结OE,如图,∵OA为⊙D的直径,
∴∠AEO=90°,
∴OE⊥AC,
∴AE=CE=2,
∴AC=4;
(2)∵AB为⊙O的直径,
∴∠ACB=90°,
∵AB=8,AC=4,
即AC=
| 1 |
| 2 |
∴∠B=30°,
即
 |
| AC |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理.

练习册系列答案
相关题目
某同学解方程5x-1=□x+3时,把□处数字看错得x=-
,他把□处看成了( )
| 3 |
| 4 |
| A、3 | B、-9 | C、8 | D、-8 |
若一次函数y=kx+b的图象经过点(-2,-1)和点(1,2),则这个函数的图象不经过( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知:点O在△ABC内,OA=OB=OC,则点O为( )
| A、两条角平分线的交点 |
| B、两条高线的交点 |
| C、两条边垂直平分线的交点 |
| D、两条边的中线的交点 |
 如图所示,从点O出发的四条射线OA、OB、OC、OD,已知∠AOC=90°,∠BOD=90°.
如图所示,从点O出发的四条射线OA、OB、OC、OD,已知∠AOC=90°,∠BOD=90°.