题目内容
 如图所示,从点O出发的四条射线OA、OB、OC、OD,已知∠AOC=90°,∠BOD=90°.
如图所示,从点O出发的四条射线OA、OB、OC、OD,已知∠AOC=90°,∠BOD=90°.(1)若∠BOC=30°,求∠AOB与∠COD的大小;
(2)若∠BOC=34°,求∠AOB与∠COD的大小;
(3)你能发现什么?
(4)你能说明你的发现吗?
考点:余角和补角
专题:
分析:(1)根据OA⊥OC得到∠AOC=90°,所以∠AOB=90°-∠BOC,同理可得∠COD的度数;
(2)与(1)的求解方法完全相同;
(3)∠AOB=∠COD相等.
(4)由∠AOB+∠BOC=∠COD+∠BOC=90°,可得到∠AOB=∠COD.
(2)与(1)的求解方法完全相同;
(3)∠AOB=∠COD相等.
(4)由∠AOB+∠BOC=∠COD+∠BOC=90°,可得到∠AOB=∠COD.
解答:解:解:(1)∵∠AOC=90°,
∴∠AOB+∠BOC=90°,
∵∠BOC=30°,
∴∠AOB+30°=90°,
∴∠AOB=60°,
同理可得:∠COD=60°.
(2)∵∠AOC=90°,
∴∠AOB+∠BOC=90°,
∵∠BOC=34°,
∴∠AOB+34°=90°,
∴∠AOB=56°,
同理可得:∠COD=56°;
(3)从(1)、(2)的运算知道:
∠AOB=∠COD.
(4)∵∠AOC=90°,∠BOD=90°,
∴∠AOB+∠BOC=90°,
∠COD+∠BOC=90°,
∴∠AOB=90°-∠BOC,
∠COD=90°-∠BOC,
∴∠AOB=∠COD.
∴∠AOB+∠BOC=90°,
∵∠BOC=30°,
∴∠AOB+30°=90°,
∴∠AOB=60°,
同理可得:∠COD=60°.
(2)∵∠AOC=90°,
∴∠AOB+∠BOC=90°,
∵∠BOC=34°,
∴∠AOB+34°=90°,
∴∠AOB=56°,
同理可得:∠COD=56°;
(3)从(1)、(2)的运算知道:
∠AOB=∠COD.
(4)∵∠AOC=90°,∠BOD=90°,
∴∠AOB+∠BOC=90°,
∠COD+∠BOC=90°,
∴∠AOB=90°-∠BOC,
∠COD=90°-∠BOC,
∴∠AOB=∠COD.
点评:本题主要考查角的运算,看懂图形,准确找出角的和差关系便不难进行求

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 如图,一个水坝的截面是梯形,坝顶宽4m,坝高为6m,迎水坡的坡度为i=1:
如图,一个水坝的截面是梯形,坝顶宽4m,坝高为6m,迎水坡的坡度为i=1: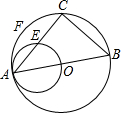 如图,已知△ABC内接于⊙O,AB为⊙O的直径,AB=8cm,以OA为直径的⊙D与⊙O的弦AC交于E点,若CE=2cm,求:
如图,已知△ABC内接于⊙O,AB为⊙O的直径,AB=8cm,以OA为直径的⊙D与⊙O的弦AC交于E点,若CE=2cm,求: