题目内容
已知抛物线y1=x2+x-k与直线y=-2x+1的交点的纵坐标为3.
(1)求抛物线的表达式;
(2)求抛物线y1=x2+x-k与直线y=-2x+1的另一个交点的坐标.
(1)求抛物线的表达式;
(2)求抛物线y1=x2+x-k与直线y=-2x+1的另一个交点的坐标.
考点:二次函数的性质
专题:计算题
分析:(1)先利用一次函数解析式确定抛物线与直线的交点坐标为(-1,3),然后把点(-1,3)代入y1=x2+x-k中求出k即可得到抛物线解析式;
(2)解由抛物线解析式和一次函数解析式所组成的方程组即可得到它们的交点坐标.
(2)解由抛物线解析式和一次函数解析式所组成的方程组即可得到它们的交点坐标.
解答:解:(1)当y=3时,-2x+1=3,解得x=-2,
则抛物线与直线的交点坐标为(-1,3),
把(-1,3)代入y1=x2+x-k得1-1-k=3,解得k=-3,
所以抛物线解析式为y1=x2+x+3;
(2)解方程组
得
或
,
所以抛物线y1=x2+x-k与直线y=-2x+1的另一个交点的坐标为(-2,5).
则抛物线与直线的交点坐标为(-1,3),
把(-1,3)代入y1=x2+x-k得1-1-k=3,解得k=-3,
所以抛物线解析式为y1=x2+x+3;
(2)解方程组
|
|
|
所以抛物线y1=x2+x-k与直线y=-2x+1的另一个交点的坐标为(-2,5).
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在直角坐标系中,如果点P(a+3,a+1)在x轴上,则P点的坐标为( )
| A、(0,2) |
| B、(2,0) |
| C、(4,0) |
| D、(0,-4) |
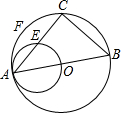 如图,已知△ABC内接于⊙O,AB为⊙O的直径,AB=8cm,以OA为直径的⊙D与⊙O的弦AC交于E点,若CE=2cm,求:
如图,已知△ABC内接于⊙O,AB为⊙O的直径,AB=8cm,以OA为直径的⊙D与⊙O的弦AC交于E点,若CE=2cm,求: