题目内容
已知：点O在△ABC内，OA=OB=OC，则点O为（ ）
| A、两条角平分线的交点 |
| B、两条高线的交点 |
| C、两条边垂直平分线的交点 |
| D、两条边的中线的交点 |
考点：线段垂直平分线的性质
专题：
分析：由点O在△ABC内，OA=OB=OC，根据线段垂直平分线的性质，即可知点O为两条边垂直平分线的交点．
解答：解：∵点O在△ABC内，OA=OB=OC，
∴点O为两条边垂直平分线的交点．
故选C．
∴点O为两条边垂直平分线的交点．
故选C．
点评：此题考查了线段垂直平分线的性质．此题比较简单，注意熟记定理是解此题的关键．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
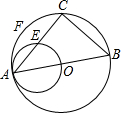如图，已知△ABC内接于⊙O，AB为⊙O的直径，AB=8cm，以OA为直径的⊙D与⊙O的弦AC交于E点，若CE=2cm，求：
在直角坐标系中，如果点P（a+3，a+1）在x轴上，则P点的坐标为（ ）
| A、（0，2） |
| B、（2，0） |
| C、（4，0） |
| D、（0，-4） |