题目内容
1.在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于D;(1)如果点F与点A重合,且∠C=50°,∠B=30°,如图1,求∠EFD的度数;
(2)如果点F在线段AE上(不与点A重合),如图2,问∠EFD与∠C-∠B有怎样的数量关系?并说明理由.
(3)如果点F在△ABC外部,如图3,此时∠EFD与∠C-∠B的数量关系是否会发生变化?请说明理由.
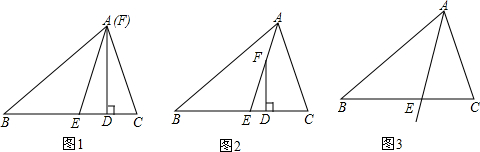
分析 (1)由三角形内角和定理可得∠BAC=100°,∠CAD=40°,由角平分线的性质易得∠EAC的度数,可得∠EFD;
(2)由角平分线的性质和三角形的内角和得出∠BAE=90°-$\frac{1}{2}$(∠C+∠B),外角的性质得出∠AEC=90°+$\frac{1}{2}$(∠B-∠C),在△EFD中,由三角形内角和定理可得∠EFD;
(3)与(2)的方法相同.
解答 (1)解:∵∠C=50°,∠B=30°,
∴∠BAC=180°-50°-30°=100°.
∵AE平分∠BAC,
∴∠CAE=50°.
在△ACE中∠AEC=80°,
在Rt△ADE中∠EFD=90°-80°=10°.
(2)∠EFD=$\frac{1}{2}$(∠C-∠B)
证明:∵AE平分∠BAC,
∴∠BAE=$\frac{180°-∠B-∠C}{2}$=90°-$\frac{1}{2}$(∠C+∠B)
∵∠AEC为△ABE的外角,
∴∠AEC=∠B+90°-$\frac{1}{2}$(∠C+∠B)=90°+$\frac{1}{2}$(∠B-∠C)
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°-90°-$\frac{1}{2}$(∠B-∠C)
∴∠EFD=$\frac{1}{2}$(∠C-∠B)
(3)∠EFD=$\frac{1}{2}$(∠C-∠B).
如图,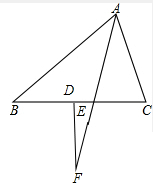
∵AE平分∠BAC,
∴∠BAE=$\frac{180°-∠B+∠C}{2}$.
∵∠DEF为△ABE的外角,
∴∠DEF=∠B+$\frac{180°-∠B+∠C}{2}$=90°+$\frac{1}{2}$(∠B-∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°-90°-$\frac{1}{2}$(∠B-∠C)
∴∠EFD=$\frac{1}{2}$(∠C-∠B).
点评 本题主要考查了三角形的内角和定理,综合利用角平分线的性质和三角形内角和定理是解答此题的关键.

| A. | 如果一个直角三角形的两条直角边与另一个直角三角形的两条直角边对应相等,那么这两个直角三角形全等 | |
| B. | 等腰三角形顶角的平分线把它分成两个全等的三角形 | |
| C. | 周长相等的两个三角形全等 | |
| D. | 有一条直角边对应相等的两个等腰直角三角形全等 |
| A. | 5与6之间 | B. | 4与5之间 | C. | 3与4之间 | D. | 2与3之间 |
| X(元/件) | 35 | 40 | 45 | 50 | 55 |
| Y(件) | 550 | 500 | 450 | 400 | 350 |
(2)设公司试销该产品每天获得的毛利润为S(元),求S与x之间的函数表达式.
(毛利润=销售总价-成本总价)
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
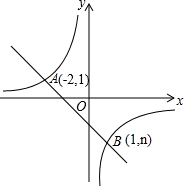 已知:如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,
已知:如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点, 如图,胶州湾大桥是一座斜拉式大桥,斜拉式大桥多采用三角形结构,使其不易变形,这种做法的依据是三角形的稳定性.
如图,胶州湾大桥是一座斜拉式大桥,斜拉式大桥多采用三角形结构,使其不易变形,这种做法的依据是三角形的稳定性.