题目内容
某校安了一个圆柱形饮水桶的支架(如图1),若不计木条的厚度,其俯视图如图2,已知AD垂直平分CB,AD=BC=36cm,则圆柱形饮水桶的底面半径的最大值是 cm.


考点:勾股定理的应用
专题:
分析:当圆柱形饮水桶的底面半径最大时,圆外接于△ABC;连接外心与B点,可通过勾股定理即可求出圆的半径.
解答:解:连接OB,如图,
当⊙O为△ABC的外接圆时圆柱形饮水桶的底面半径的最大.
∵AD垂直平分BC,AD=BC=36cm,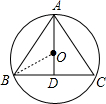
∴O点在AD上,BD=18cm;
在Rt△0BD中,设半径为r,则OB=r,OD=36-r,
∴r2=(36-r)2+182,解得r=22.5.
即圆柱形饮水桶的底面半径的最大值为22.5cm.
故答案为:30.
当⊙O为△ABC的外接圆时圆柱形饮水桶的底面半径的最大.
∵AD垂直平分BC,AD=BC=36cm,

∴O点在AD上,BD=18cm;
在Rt△0BD中,设半径为r,则OB=r,OD=36-r,
∴r2=(36-r)2+182,解得r=22.5.
即圆柱形饮水桶的底面半径的最大值为22.5cm.
故答案为:30.
点评:此题主要考查了垂径定理的推论和勾股定理,具备把实物图转化为几何图形的能力是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
今年我国发现的首例H7N9禽流感确诊病例在某医院隔离观察,要掌握他在一周内的体温变化情况宜采用( )
| A、条形统计图 |
| B、扇形统计图 |
| C、频数直方图 |
| D、折线统计图 |
下列多项式不能用完全平方公式分解的是( )
| A、x2+4x+4 |
| B、y4-8y2+16 |
| C、x2-2x+4 |
| D、4y2-12y+9 |
 如图在△ABC中,∠C=90°,∠B=30°.点D为AB的中点,DE⊥AB,交BC于E,如果DE=1cm,那么AC的长度为
如图在△ABC中,∠C=90°,∠B=30°.点D为AB的中点,DE⊥AB,交BC于E,如果DE=1cm,那么AC的长度为