题目内容
8.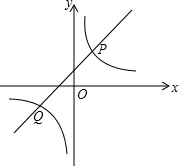 如图,直线y=k1x+1与双曲线y=$\frac{{k}_{2}}{x}$相交于P(1,m),Q(-2,-1)两点;
如图,直线y=k1x+1与双曲线y=$\frac{{k}_{2}}{x}$相交于P(1,m),Q(-2,-1)两点;(1)求m的值;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1,y2,y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+1>$\frac{{k}_{2}}{x}$的解集.
分析 (1)把把Q(-2,-1)代入反比例函数的解析式求得函数解析式,然后把P代入求得m的值;
(2)根据反比例函数的图象,根据自变量的相对位置,结合图象即可确定;
(3)不等式k1x+1>$\frac{{k}_{2}}{x}$的解集就是对相同的x的值,一次函数的图象在上边的部分x的范围.
解答 解:(1)把Q(-2,-1)代入y=$\frac{{k}_{2}}{x}$得:k2=2,
则反比例函数的解析式是y=$\frac{2}{x}$,
把P(1,m)代入反比例函数的解析式得:m=2;
(2)根据图象可得:y2<y1<y3;
(3)根据图象可得,解集是:-2<x<0或x>1.
点评 本题综合考查一次函数与反比例函数的图象与性质,同时考查用待定系数法求函数解析式.本题需要注意无论是自变量的取值范围还是函数值的取值范围,都应该从交点入手思考.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
19.sin45°-cos60°等于( )
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\frac{\sqrt{3}-1}{3}$ | C. | $\frac{\sqrt{2}-1}{2}$ | D. | $\frac{\sqrt{3}-\sqrt{3}}{2}$ |
8. 如图,若O为EH的中点,要使△EOF≌△HOG,不能加什么条件( )
如图,若O为EH的中点,要使△EOF≌△HOG,不能加什么条件( )
 如图,若O为EH的中点,要使△EOF≌△HOG,不能加什么条件( )
如图,若O为EH的中点,要使△EOF≌△HOG,不能加什么条件( )| A. | FO=GO | B. | AB∥CD | C. | ∠AFG=∠FGD | D. | EF=GH |


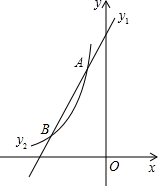 如图,已知一次函数y1=2x-3k的图象与反比例函数y2=$\frac{k-2}{x}$(x<0)的图象在第二象限内相交于A、B两点,其中点A的纵坐标为4.
如图,已知一次函数y1=2x-3k的图象与反比例函数y2=$\frac{k-2}{x}$(x<0)的图象在第二象限内相交于A、B两点,其中点A的纵坐标为4.