题目内容
3.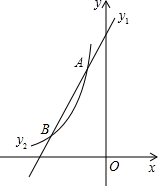 如图,已知一次函数y1=2x-3k的图象与反比例函数y2=$\frac{k-2}{x}$(x<0)的图象在第二象限内相交于A、B两点,其中点A的纵坐标为4.
如图,已知一次函数y1=2x-3k的图象与反比例函数y2=$\frac{k-2}{x}$(x<0)的图象在第二象限内相交于A、B两点,其中点A的纵坐标为4.(1)求反比例函数和一次函数的解析式;
(2)结合图象求出y1<y2时,x的取值范围.
分析 (1)把y=6代入两个函数解析式,可得到两个关于m,k的方程组,进而求解;
(2)让两个函数解析式组成方程组求得求得交点坐标,通过观察图象,找出y1<y2时,x的取值范围.
解答 解:(1)由已知,设交点A(m,4)
则有$\left\{\begin{array}{l}{2m-3k=4}\\{4m=k-2}\end{array}\right.$
解得$\left\{\begin{array}{l}{m=-1}\\{k=-2}\end{array}\right.$
∴y1=2x+6,y2=-$\frac{4}{x}$;
(2)由方程组$\left\{\begin{array}{l}{y=2x+6}\\{y=-\frac{4}{x}}\end{array}\right.$,得x2+3x+2=0
解得x1=-1,x2=-2,
由图象,可知当x<-2或-1<x<0时,y1<y2.
点评 此题主要考查一次函数与反比例函数的性质及解析式的求法.需注意:无论是自变量的取值范围还是函数值的取值范围,都应该从交点入手思考.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.无理数4$\sqrt{3}$-3在哪个整数之间( )
| A. | 1与2 | B. | 2与3 | C. | 3与4 | D. | 4与5 |
12.下列变量之间的关系不是函数关系的是( )
| A. | 长方形的面积一定,其长与宽 | B. | 正方形的周长与面积 | ||
| C. | 长方形的周长与面积 | D. | 圆的面积与圆的半径 |
 如图,已知函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,p是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,求满足条件的P点坐标.
如图,已知函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,p是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,求满足条件的P点坐标. 如图,在△ABC中,∠BAC=90°,AC=6,BC=10,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E、D,则DE的长为( )
如图,在△ABC中,∠BAC=90°,AC=6,BC=10,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E、D,则DE的长为( )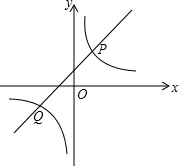 如图,直线y=k1x+1与双曲线y=$\frac{{k}_{2}}{x}$相交于P(1,m),Q(-2,-1)两点;
如图,直线y=k1x+1与双曲线y=$\frac{{k}_{2}}{x}$相交于P(1,m),Q(-2,-1)两点; 如图,正方形ABCD内的△BEC为正三角形,求∠DEA的度数.
如图,正方形ABCD内的△BEC为正三角形,求∠DEA的度数.