题目内容
20．在梯形ABCD中，AD∥BC，对角线AC、BD，相交于点O，那么S△AOB=S△COD（填“=”、“＞”、“＜”）分析 作AE⊥BC于E，由AD∥BC，得出△ABC的面积=△DCB的面积，即可得出结论．
解答 解：作AE⊥BC于E，如图所示：
∵AD∥BC，
∴△ABC的面积=$\frac{1}{2}$BC•AE，△DCB的面积=$\frac{1}{2}$BC•AE，
∴△ABC的面积=△DCB的面积，
∴△AOB的面积=△COD的面积，
即S△AOB=S△COD，
故答案为：=．
点评 本题考查了梯形的性质以及三角形面积的计算方法；由梯形的性质得出△ABC的面积=△DCB的面积是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
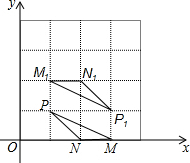在平面直角坐标系中，点P（1，1），N（2，0），△MNP和△M1N1P1的顶点都在格点上，△MNP与△M1N1P1是关于某一点中心对称，则对称中心的坐标为（2，1）．
11．无理数4$\sqrt{3}$-3在哪个整数之间（ ）
| A． | 1与2 | B． | 2与3 | C． | 3与4 | D． | 4与5 |
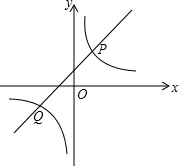如图，直线y=k1x+1与双曲线y=$\frac{{k}_{2}}{x}$相交于P（1，m），Q（-2，-1）两点；
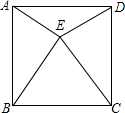如图，正方形ABCD内的△BEC为正三角形，求∠DEA的度数．
12．下列变量之间的关系不是函数关系的是（ ）
| A． | 长方形的面积一定，其长与宽 | B． | 正方形的周长与面积 | ||
| C． | 长方形的周长与面积 | D． | 圆的面积与圆的半径 |
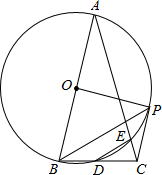如图，在△ABC中，AB=AC，∠A=30°，以AB为直径的⊙O交BC于点D，交AC于点E，过点B作∠DBP=30°，交⊙O于点P，连接DE、CP、OP．