题目内容
17.如图,在数轴上点A、B、C表示的数分别为-2、1、6,点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC
(1)请直接写出AB、BC、AC的长度;
(2)若点D从A点出发,以每秒1个单位长度的速度向左运动,点E从B点出发以每秒2个单位长度的速度向右运动,点F从C点出发以每秒5个单位长度的速度向右运动.设点D、E、F同时出发,运动时间为t秒,试探索:EF-DE的值是否随着时间t的变化而变化?请说明理由.
(3)若点M以每秒4个单位的速度从A点出发,点N以每秒3个单位的速度运动从C点出发,设点M、N同时出发,运动时间为t秒,试探究:经过多少秒后,点M、N两点间的距离为14个单位.
分析 (1)根据两点间的距离公式即可求解;
(2)用t表示出EF、DE,计算即可求解;
(3)分4种情况:①点M、N同时向左出发;②点M向左出发,点N向右出发;③点M向右出发、点N向左出发;④点M、N同时向右出发;根据等量关系点M、N两点间的距离为14个单位列出方程求解即可.
解答 解:(1)∵在数轴上点A、B、C表示的数分别为-2、1、6,
∴AB=1-(-2)=3,
BC=6-1=5,
AC=6-(-2)=8;
(2)不变,
点D、E、F同时出发,运动t秒时,D点表示的数为-2-t,E点表示的数为1+2t,F点表示的数为6+5t,
则EF=(6+5t)-(1-2t)=5+3t,DE=(1+2t)-(-2-t)=3+3t,
EF-DE=(5+3t)-(3+3t)=2,
故EF-DE的值不随着时间t的变化而改变;
(3)①点M、N同时向左出发,依题意有
4t-3t=14-8,
解得t=6;
②点M向左出发,点N向右出发,依题意有
4t+3t=14-8,
解得t=$\frac{6}{7}$;
③点M向右出发、点N向左出发,依题意有
4t+3t=14+8,
解得t=$\frac{22}{7}$;
④点M、N同时向右出发,依题意有
4t-3t=14+8,
解得t=22.
故经过6秒或$\frac{6}{7}$秒或$\frac{22}{7}$秒或22秒后,点M、N两点间的距离为14个单位.
点评 本题考查了一元一次方程的应用,数轴,根据题目给出的条件,找出合适的等量关系列出方程,再求解.(3)对点M、N的方向分类讨论是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2. 直线a、b、c、d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )
直线a、b、c、d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )
 直线a、b、c、d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )
直线a、b、c、d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )| A. | 80° | B. | 65° | C. | 60° | D. | 55° |
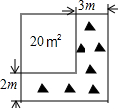 如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长是( )
如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长是( ) 如图有一个长方体的长,宽,高分别是6,4,4,在地面A处有一只蚂蚁,它想吃到长方体上面B处的事物,需要爬行的最短路程是多少?
如图有一个长方体的长,宽,高分别是6,4,4,在地面A处有一只蚂蚁,它想吃到长方体上面B处的事物,需要爬行的最短路程是多少?

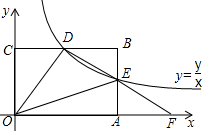 如图,点O是平面直角坐标系的原点,反比例函数y=$\frac{k}{x}$位于第一象限的图象经过矩形ABCO边AB的中点E,与边BC交于点D,连接OD,DE,延长DE与x轴交于点F,则△ODF与矩形ABCO的面积比是$\frac{3}{4}$.
如图,点O是平面直角坐标系的原点,反比例函数y=$\frac{k}{x}$位于第一象限的图象经过矩形ABCO边AB的中点E,与边BC交于点D,连接OD,DE,延长DE与x轴交于点F,则△ODF与矩形ABCO的面积比是$\frac{3}{4}$.