题目内容
5. 如图有一个长方体的长,宽,高分别是6,4,4,在地面A处有一只蚂蚁,它想吃到长方体上面B处的事物,需要爬行的最短路程是多少?
如图有一个长方体的长,宽,高分别是6,4,4,在地面A处有一只蚂蚁,它想吃到长方体上面B处的事物,需要爬行的最短路程是多少?
分析 做此题要把这个长方体中蚂蚁所走的路线放到一个平面内,在平面内线段最短,根据勾股定理即可计算.
解答 解:第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是8cm和6cm,
则所走的最短线段是$\sqrt{{6}^{2}+{8}^{2}}$=10cm;
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是10cm和4cm,
所以走的最短线段是$\sqrt{1{0}^{2}+{4}^{2}}$=2$\sqrt{29}$cm;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是10cm和4cm,
所以走的最短线段是$\sqrt{1{0}^{2}+{4}^{2}}$=2$\sqrt{29}$cm;
三种情况比较而言,第一种情况最短.
故爬行的最短路程是10cm.
点评 本题考查了平面展开-最短路径问题,此题的关键是明确两点之间线段最短这一知识点,然后把立体的长方体放到一个平面内,求出最短的线段.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
15. 有一种足球是由32块黑白相间的牛皮缝制而成的,黑皮可看作正五边形,白皮可看作正六边形(正多边形为各边相等,各内角相等的几何图形),那么白皮、黑皮的块数为( )
有一种足球是由32块黑白相间的牛皮缝制而成的,黑皮可看作正五边形,白皮可看作正六边形(正多边形为各边相等,各内角相等的几何图形),那么白皮、黑皮的块数为( )
 有一种足球是由32块黑白相间的牛皮缝制而成的,黑皮可看作正五边形,白皮可看作正六边形(正多边形为各边相等,各内角相等的几何图形),那么白皮、黑皮的块数为( )
有一种足球是由32块黑白相间的牛皮缝制而成的,黑皮可看作正五边形,白皮可看作正六边形(正多边形为各边相等,各内角相等的几何图形),那么白皮、黑皮的块数为( )| A. | 18、14 | B. | 16、16 | C. | 20、12 | D. | 22、10 |
20.一个蓄水池有15m3的水,以每分钟0.5m3的速度向池中注水,蓄水池中的水量Q(m3)与注水时间t(分)间的函数表达式为( )
| A. | Q=0.5t | B. | Q=15t | C. | Q=15+0.5t | D. | Q=15-0.5t |
14.下列说法正确的是( )
| A. | 若AB=2AC,则点C是线段AB的中点 | |
| B. | 一条射线把一个角分成两个角,这条射线是这个角的平分线 | |
| C. | 点到直线的距离是指从直线外一点到这条直线的垂线的长度 | |
| D. | 在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线 |
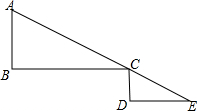 点A、C、E在一条直线上,在Rt△ABC和Rt△CDE中,∠B=∠D=90°,AB=3,CD=$\sqrt{3}$,∠ACB=∠E=30°,△CDE绕C顺时针旋转角度为α(0<α<180°),旋转过程中,直线DE分别与直线AC、直线BC交于M、N两点,当MN=MC时,则NB=$\sqrt{3}$.
点A、C、E在一条直线上,在Rt△ABC和Rt△CDE中,∠B=∠D=90°,AB=3,CD=$\sqrt{3}$,∠ACB=∠E=30°,△CDE绕C顺时针旋转角度为α(0<α<180°),旋转过程中,直线DE分别与直线AC、直线BC交于M、N两点,当MN=MC时,则NB=$\sqrt{3}$.
