题目内容
已知:抛物线经过A(0,3),B(1,-4),C(-2,5)三点,求:
(1)抛物线的解析式;
(2)抛物线的开口方向、对称轴、顶点坐标.
(1)抛物线的解析式;
(2)抛物线的开口方向、对称轴、顶点坐标.
考点:待定系数法求二次函数解析式,二次函数的性质
专题:
分析:(1)先二次函数的解析式为y=ax2+bx+c(a、b、c为常数,a≠0),再把点(0,3)、(1,-1)、(-1,9)代入得到关于a、b、c的方程组,然后解方程组求出a、b、c的值.
(2)把一般式转化成顶点式,从而根据a的值判定开口方向,根据顶点式得出对称轴和顶点坐标.
(2)把一般式转化成顶点式,从而根据a的值判定开口方向,根据顶点式得出对称轴和顶点坐标.
解答:解:(1)设二次函数的解析式为y=ax2+bx+c(a、b、c为常数,a≠0),
把点(0,3)、(1,-4)、(-2,5)代入得
,
解得
,
所以抛物线的解析式为y=-2x2-5x+3.
(2)∵a=-<0,
∴抛物线的开口向下,
∵y=-2x2-5x+3=-2(x+
)2+
,
∴抛物线的对称轴为x=
,顶点坐标为(-
,
).
把点(0,3)、(1,-4)、(-2,5)代入得
|
解得
|
所以抛物线的解析式为y=-2x2-5x+3.
(2)∵a=-<0,
∴抛物线的开口向下,
∵y=-2x2-5x+3=-2(x+
| 5 |
| 4 |
| 49 |
| 8 |
∴抛物线的对称轴为x=
| 5 |
| 4 |
| 5 |
| 4 |
| 49 |
| 8 |
点评:本题考查了二次函数的性质以及待定系数法求二次函数的解析式:设二次函数的解析式为y=ax2+bx+c(a、b、c为常数,a≠0),再把函数图象上三个点的坐标代入得到关于a、b、c的方程组,解方程组求出a、b、c的值,从而确定二次函数的解析式.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知直线y=2x与直线y=kx+5互相平行,则k的值为( )
| A、k=-2 | B、k=2 |
| C、k=±2 | D、无法确定k的值 |
下列式子中,化简结果正确的是( )
| A、-|-5|=5 | ||||
| B、|-5|=5 | ||||
C、|-0.5|=-
| ||||
D、+(-
|
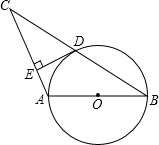 已知:如图,AB为⊙O的直径,⊙O过BC的中点D,且DE⊥AC,
已知:如图,AB为⊙O的直径,⊙O过BC的中点D,且DE⊥AC, 如图,已知⊙O内
如图,已知⊙O内