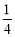题目内容
(本题9分)如图,对称轴为x=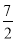 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
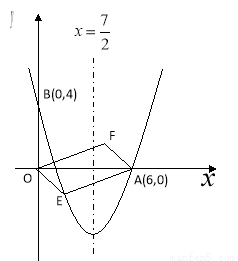
(1)求抛物线解析式;
(2)设点E(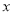 ,
,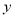 )是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与
)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与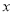 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量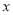 的取值范围;
的取值范围;
①当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?
②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
(1)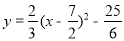 (2)见解析
(2)见解析
【解析】
试题分析:(1)理由待定系数法进行求解,将解析式设为顶点式,然后计算;(2)根据四边形的面积求出点E的坐标,然后分别进行判断;(3)根据正方形的性质求出点E的坐标,然后进行说明.
试题解析:(1)设抛物线的解析式为y=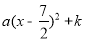 .
.
把A、B两点坐标代入上式,得 解得
解得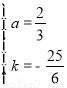 .
.
所以抛物线的解析式为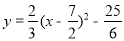 .
.
(2)因为点E(x,y)在抛物线上,位于第四象限,且坐标适合抛物线的解析式,
所以y<0,即-y>0,-y表示点E到OA的距离.
因为OA是平行四边形OEAF的对角线,所以S=2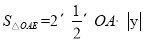 =-6y=-4
=-6y=-4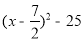
因为抛物线与x轴的两个交点是(1,0)和(6,0),所以,自变量x的取值范围是1<x<6.
①依题意,当S=24时,即-4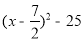 =24,解得
=24,解得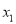 =3,
=3,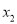 =4.
=4.
所以点E的坐标为(3,-4)或(4,-4).
E(3,-4)满足OE=AE,所以四边形OEAF是菱形;
E(4,-4)不满足OE=AE,所以四边形OEAF不是菱形.
②当OA⊥EF,且OA=EF时,四边形OEAF是正方形,此时点E的坐标只能是(3,-3),而点(3,-3)不在抛物线上,故不存在这样的点E,使四边形OEAF是正方形.
考点:待定系数法求二次函数的解析式、菱形与正方形的性质.

练习册系列答案
相关题目
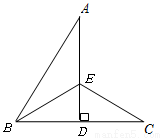
 ,则BC的长是( )
,则BC的长是( )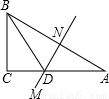
 人,平均每人占有粮食数为
人,平均每人占有粮食数为 吨,则
吨,则 与
与 之间的函数图象大致是( )
之间的函数图象大致是( )
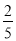 ,则n=___________。
,则n=___________。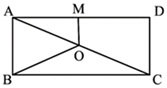
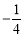 D、2?2=
D、2?2=