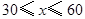题目内容
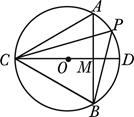
如图,已知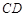 是⊙
是⊙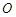 的直径,弦
的直径,弦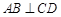 ,垂足为点
,垂足为点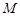 ,点
,点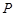 是
是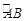 上一点,且
上一点,且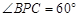 .
.
试判断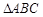 的形状,并说明你的理由.
的形状,并说明你的理由.
依据等边三角形的三角相等来求证三角形
解析试题分析:解:方法一: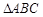 为等边三角形 1分
为等边三角形 1分
∵AB⊥CD,CD为⊙O的直径
∴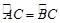 3分
3分
∴AC=BC 4分
又∵在⊙O中,∠BPC=∠A 5分
∵∠BPC=60°
∴∠A=60° 7分
∴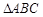 为等边三角形 8分
为等边三角形 8分
方法二: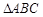 为等边三角形 1分
为等边三角形 1分
∵AB⊥CD,CD为⊙O的直径
∴AM=BM 3分
即CD垂直平分AB
∴AC=BC 4分
又∵在⊙O中,∠BPC=∠A 5分
∵∠BPC=60°
∴∠A=60° 7分
∴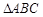 为等边三角形
为等边三角形
考点:等边三角形的求法
点评:等边三角形的基本性质是三个角是60,并且是通过做垂线,垂线垂直且平分底边

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目

 是⊙O的直径,
是⊙O的直径, 是弦,过点
是弦,过点 作OD⊥AC于
作OD⊥AC于 ,连结
,连结 .
.
 ;
; ,求∠
,求∠ 的度数.
的度数. 是⊙O的直径,直线
是⊙O的直径,直线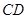 与⊙O相切于
与⊙O相切于 点,
点,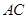 平分
平分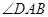 .
. 
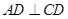 ;
;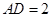 ,
,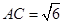 ,求⊙O的半径长.
,求⊙O的半径长.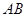 是⊙O的直径,直线
是⊙O的直径,直线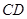 与⊙O相切于
与⊙O相切于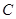 点,
点,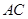 平分
平分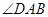 .
.

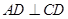 ;
;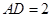 ,
,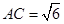 ,求⊙O的半径长.
,求⊙O的半径长.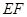 是⊙O的直径,把
是⊙O的直径,把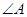 为
为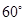 的直角三角板
的直角三角板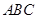 的一条直角边
的一条直角边 放在直线
放在直线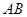 与⊙O交于点
与⊙O交于点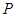 ,点
,点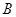 与点
与点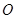 重合.将三角板
重合.将三角板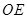 方向平移,使得点
方向平移,使得点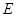 重合为止.设
重合为止.设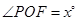 ,则
,则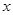 的取值范围是( )
的取值范围是( )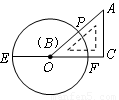
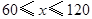 B.
B.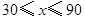 C.
C.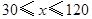 D.
D.