题目内容
已知△ABC的各边长度分别为3cm,4cm,5cm,则这个三角形外接圆的半径为( )
| A、2cm | B、2.4cm |
| C、2.5cm | D、6cm |
考点:三角形的外接圆与外心,勾股定理的逆定理
专题:
分析:由在△ABC中,AC=4cm,BC=3cm,AB=5cm,可判定△ABC是直角三角形,然后由直角三角形的斜边即是它的外接圆的直径,求得答案.
解答:解:∵在△ABC中,AC=4cm,BC=3cm,AB=5cm,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,且AB是斜边,
∴△ABC的外接圆半径长为:
AB=2.5cm.
故选C.
∴AB2=AC2+BC2,
∴△ABC是直角三角形,且AB是斜边,
∴△ABC的外接圆半径长为:
| 1 |
| 2 |
故选C.
点评:此题考查了三角形的外接圆与勾股定理的逆定理.此题难度不大,注意判定△ABC是直角三角形是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在平面直角坐标系中,点O是坐标原点,点A是x轴正半轴上的一个动点,过A点作y轴的平行线交反比例函数y=
(x>0)的图象于B点,当点A的横坐标逐渐增大时,△OAB的面积将会( )
| 2 |
| x |
| A、逐渐增大 | B、逐渐减小 |
| C、不变 | D、先增大后减小 |
设m>n>0,m2+n2=3mn,则
的值等于( )
| m2-n2 |
| mn |
A、2
| ||
B、
| ||
C、2
| ||
D、
|
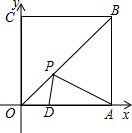 如图所示,四边形OABC为正方形,边长为3,点A、C分别在x轴,y轴的正半轴上,点D在OA上,且D点的坐标为(1,0),P是OB上的一个动点,则PD+PA和的最小值是( )
如图所示,四边形OABC为正方形,边长为3,点A、C分别在x轴,y轴的正半轴上,点D在OA上,且D点的坐标为(1,0),P是OB上的一个动点,则PD+PA和的最小值是( )A、2
| ||
B、
| ||
| C、4 | ||
| D、9 |
 图中几何体的主视图是( )
图中几何体的主视图是( )A、 |
B、 |
C、 |
D、 |
已知正比例函数y=-4x与反比例函数y=
的图象交于A、B两点,若点A(m,4),则点B的坐标为( )
| k |
| x |
| A、(1,-4) |
| B、(-1,4) |
| C、(4,-1) |
| D、(-4,1) |
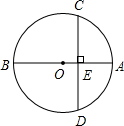 已知,AB为⊙O的直径,弦CD⊥AB,E为垂足.若BE=6,AE=4,则CD=
已知,AB为⊙O的直径,弦CD⊥AB,E为垂足.若BE=6,AE=4,则CD= 将两个全等的直角三角形,拼成一个四边形.问:这些四边形中有几个轴对称图形,有几个中心对称图形?
将两个全等的直角三角形,拼成一个四边形.问:这些四边形中有几个轴对称图形,有几个中心对称图形? 在Rt△ABC中,∠C=90°,点D为BC边上一点,CD=1,且cos∠ADC=
在Rt△ABC中,∠C=90°,点D为BC边上一点,CD=1,且cos∠ADC=