Question

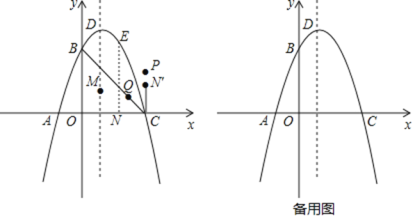
【题目】在平面直角坐标系xoy中，已知 A(4，0)、B(1，3)， 过的直线是绕着△OAB的顶点A旋转，与y轴相交于点P，探究解决下列问题：

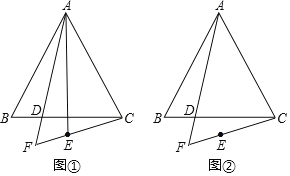
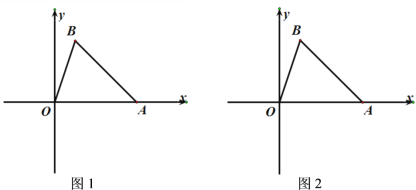
（1）如图1所示，当直线旋转到与边OB相交时，试用无刻度的直尺和圆规确定点P的位置，使顶点O、B到直线的距离之和最大，（保留作图痕迹）；

（2）当直线旋转到与y轴的负半轴相交时，使顶点O、B到直线的距离之和最大，请直接写出点P的坐标是 ．（可在图2中分析）

Answer 1

【答案】（1）详见解析；（2）（0，）．

【解析】

（1）如图1，过A点作直线⊥OB于点F，与y轴的交点即为所确定的P点位置．

过点O作OD⊥于D，过点B作BC⊥于C．利用三角形的面积公式得到为定值，FA取最小值即可．由垂线段最短入手进行解答；

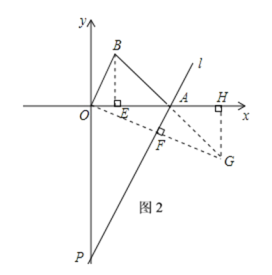
（2）如图2所示，延长BA到G点，使BA=AG，联结OG，结合（1）问得到到的距离之和最大时的位置，过点B作BE⊥OA于点E，过点G作GH⊥x轴于点H，利用三角形全等得到相关数量关系，再利用等角的三角函数可得答案．

（1）、如图1，过A点作直线⊥OB于点F，与y轴的交点即为所确定的P点位置．

理由如下：

如图1所示，过点O作OD⊥于D，过点B作BC⊥于C．

∵为定值．

要使点O、B到直线l的距离之和最大，即OD+BC最大，

只要使FA最小，

∴过A点作直线⊥OB于点F，此时FA即为最小值（此时，点F、D、C重合）．

∴与y轴的交点即为所确定的P点位置；

尺规作图如下图；

（2）、如图2所示，延长BA到G点，使BA=AG，联结OG，

则 旋转直线 至⊥OG于点F，

此时，关于点对称，

到的距离相等，

由（1）知：到的距离之和最大，

所以：到的距离之和最大，

所以与y轴的交点即为所确定的P点，

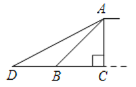
过点B作BE⊥OA于点E， ∵B（1，3），A（4，0），

∴EB=EA=3．

过点G作GH⊥x轴于点H，

∴△ABE≌△AGH（AAS），

∴AH=3，GH=3，

∴OH=7， ∴tan∠HOG=

又∵直线⊥OG于点F，

∴∠OPA=∠HOG，

∴tan∠OPA=tan∠HOG=，

∴ ，

∴ 3 OP =28， ∴OP=

∴P（0，）．