��Ŀ����
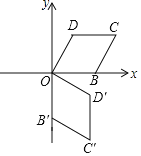
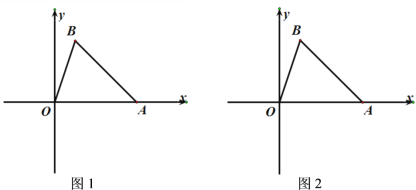
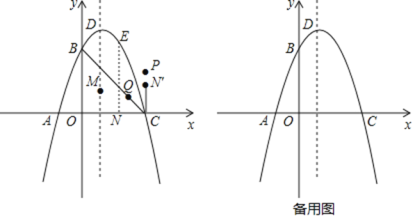
����Ŀ����ͼ����ƽ��ֱ������ϵ�ڣ�������![]() ��x�ύ�ڵ�A��C����A�ڵ�C����ࣩ����y�ύ�ڵ�B������ΪD.��QΪ�߶�BC�����ȷֵ㣨������C��.
��x�ύ�ڵ�A��C����A�ڵ�C����ࣩ����y�ύ�ڵ�B������ΪD.��QΪ�߶�BC�����ȷֵ㣨������C��.
��1����MΪ�����߶Գ�����һ�㣬��EΪ�Գ����Ҳ��������ϵĵ���λ�ڵ�һ���ޣ���![]() ���ܳ���Сʱ����
���ܳ���Сʱ����![]() ��������ֵ��
��������ֵ��
��2���ڣ�1���������£���![]() ��������ʱ������E��
��������ʱ������E��![]() �ᣬ����ΪN�����߶�CN�Ƶ�C˳ʱ����ת90���õ���N���ٽ���N����ƽ��
�ᣬ����ΪN�����߶�CN�Ƶ�C˳ʱ����ת90���õ���N���ٽ���N����ƽ��![]() ����λ����.�õ���P����G�������ߵĶԳ����ϣ�������ƽ��ֱ������ϵ���Ƿ����һ��H��ʹ��D��P��G��H��������.�����ڣ���ֱ��д����H�����꣬�������ڣ���˵������.
����λ����.�õ���P����G�������ߵĶԳ����ϣ�������ƽ��ֱ������ϵ���Ƿ����һ��H��ʹ��D��P��G��H��������.�����ڣ���ֱ��д����H�����꣬�������ڣ���˵������.
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ��
��![]()
��������
��1������QA�������߶Գ�����M����ʱ��MQC�ܳ���С�������M��1��![]() ���������ֱ��CM����ʽy=-
���������ֱ��CM����ʽy=-![]() x+1�����E��t��-t2+2t+3��������S��ECM=
x+1�����E��t��-t2+2t+3��������S��ECM=![]() ES��C������-M���������ɵó�S��ECM=-��t-
ES��C������-M���������ɵó�S��ECM=-��t-![]() ��2+
��2+![]() ����S��CME���ֵ=
����S��CME���ֵ=![]() ��
��
��2��������������P��3��2���������������빫ʽ�ɶ�����DP=2![]() �����������ʵ�PH��DG��y�ᣬPH=DP=2
�����������ʵ�PH��DG��y�ᣬPH=DP=2![]() ��������������ٵ�H�ڵ�P�Ϸ����ڵ�H�ڵ�P�·���
��������������ٵ�H�ڵ�P�Ϸ����ڵ�H�ڵ�P�·���
��1����y=0����-x2+2x+3=0�����x1=-1��x2=3��
��A��-1��0����C��3��0����
��x=0����y=3��
��B��0��3����
��ͼ1����Q��QF��x����F��

��QF��OB��
���CQF�ס�CBO��
��![]()
�ߵ�QΪ�߶�BC�����ȷֵ㣨������C����
��![]()
��![]() ��
��
��QF=CF=1��
��Q��2��1����
��y=-x2+2x+3=-��x-1��2+4��
��D��1��4���������߶Գ���x=1
����AQ�������߶Գ�����M����M��1��![]() ������ʱ��MQC�ܳ���С��
������ʱ��MQC�ܳ���С��
��ֱ��CM����ʽΪy=kxb���� ����ã�
����ã� ��
��
��y=-![]() x+1��
x+1��
��E��t��-t2+2t+3��Ϊ�����߶Գ����Ҳ���λ�ڵ�һ�����ڵĵ㣬��E��EN��x����N��EN��CM��S��
��S��t��-![]() t+1����
t+1����
��ES=-t2+2t+3-��-![]() t+1��=-t2+
t+1��=-t2+![]() t+2��
t+2��
��S��CME��![]() ��2ES=-t2+
��2ES=-t2+![]() t+2=-��t-
t+2=-��t-![]() ��2+
��2+![]() ��
��
��-1��0��
�൱t=![]() ʱ��S��CME���ֵ=
ʱ��S��CME���ֵ=![]() ��
��
��2�����ڣ���ͼ2���ɣ�1��֪CN=OC-ON=3-![]() =
=![]() ������ת��CN��=CN=
������ת��CN��=CN=![]() ��CN����x�ᣬ
��CN����x�ᣬ

�������CP��x�ᣬCP=CN��+N��P=2��
��P��3��2��
��DP=![]() ��
��
���ı���DPHG�����Σ�
��DG=PH=DP=2![]() ��PH��DG��
��PH��DG��
��H��3��2-2![]() ����
����
��ͼ3��

���ı���DPHG�����Σ�
��DG=PH=DP=2![]() ��PH��DG��
��PH��DG��
��H��3��2+2![]() ����
����
��ͼ4���ı���DPGH�����Σ�P��H���������߶Գ���Գƣ�

��H��-1��2����
��ͼ5������P��PG��ֱ��x=1��G����DH��ֱ��x=1����P��PH��DH��H��

��PH=DG=DH=PG=2����PGD=90��
���ı���DPGH�����Σ�
��H��3��4��
������������H��������3��2-2![]() ����3��2+2
����3��2+2![]() ����-1��2����3��4����
����-1��2����3��4����

 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д� Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�