题目内容
3.已知10x=m,10y=n,则102x+3y等于m2n3.分析 先根据同底数幂的乘法进行变形,再根据幂的乘方变形,最后整体代入求出即可.
解答 解:∵10x=m,10y=n,
∴102x+3y
=102x×103y
=(10x)2×(10y)3
=m2n3.
故答案为:m2n3.
点评 本题考查了同底数幂的乘法,幂的乘方的应用,能灵活运用法则进行变形是解此题的关键,用了整体代入思想.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
14.下列说法中,正确的是( )
| A. | 2不是单项式 | B. | -ab2的系数是-1,次数是3 | ||
| C. | 6πx3的系数是6 | D. | -$\frac{{2{x^2}y}}{3}$的系数是-2 |
15.$\sqrt{43}$介于哪两个整数之间( )
| A. | 4与5 | B. | 5与6 | C. | 6与7 | D. | 7与8 |
12.让我们做一个数学游戏:
第一步:取一个自然数n1=5,计算n${\;}_{1}^{2}$+1得a1
第二步:算出a1的各位数字之和得n2,计算n${\;}_{2}^{2}$+1得a2
第三步:算出a2的各位数字之和得n3,计算n${\;}_{3}^{2}$+1得a3;
依此类推,则a2014的值为( )
第一步:取一个自然数n1=5,计算n${\;}_{1}^{2}$+1得a1
第二步:算出a1的各位数字之和得n2,计算n${\;}_{2}^{2}$+1得a2
第三步:算出a2的各位数字之和得n3,计算n${\;}_{3}^{2}$+1得a3;
依此类推,则a2014的值为( )
| A. | 26 | B. | 65 | C. | 122 | D. | 不能确定 |
13.已知x=2是关于x的方程3x+a=1的解,则a的值是( )
| A. | 5 | B. | -5 | C. | 7 | D. | -7 |
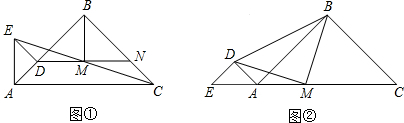
 如图,?ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长为2.
如图,?ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长为2. 如图所示,直线CD、EF被直线AB所截,若∠AMC=∠BNF,则∠CMN+∠MNE=180°.
如图所示,直线CD、EF被直线AB所截,若∠AMC=∠BNF,则∠CMN+∠MNE=180°.