题目内容
 如图I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E,
如图I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E,(1)BE与IE相等吗?为什么?(2)试说明IE是AE和DE的比例中项.
分析:(1)利用内心的性质得出∠1=∠2,∠3=∠5,再利用外角性质得出∠BIE=∠EBI,进而求出即可;
(2)利用相似三角形的性质与判定得出△BED∽△AEB,进而求出BE2=AE•ED,即可得出答案.
(2)利用相似三角形的性质与判定得出△BED∽△AEB,进而求出BE2=AE•ED,即可得出答案.
解答: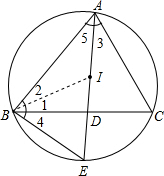 解:①BE=IE
解:①BE=IE
证明:连接BI.
∵I为△ABC内心,
∴∠1=∠2,
∠3=∠5,
∵∠3=∠4,
∴∠4=∠5,
∵∠BIE=∠2+∠5,
∠EBI=∠1+∠4,
∴∠BIE=∠EBI,
∴BE=IE;
②证明:∵∠BED=∠AEB,
∠4=∠5,
∴△BED∽△AEB,
∴
=
即 BE2=AE•ED,
由①知BE=IE,
∴IE2=AE•ED,
∴IE是AE和DE的比例中项.
 解:①BE=IE
解:①BE=IE 证明:连接BI.
∵I为△ABC内心,
∴∠1=∠2,
∠3=∠5,
∵∠3=∠4,
∴∠4=∠5,
∵∠BIE=∠2+∠5,
∠EBI=∠1+∠4,
∴∠BIE=∠EBI,
∴BE=IE;
②证明:∵∠BED=∠AEB,
∠4=∠5,
∴△BED∽△AEB,
∴
| BE |
| AE |
| ED |
| EB |
由①知BE=IE,
∴IE2=AE•ED,
∴IE是AE和DE的比例中项.
点评:此题主要考查了三角形内心的性质以及三角形外角的性质和相似三角形的判定与性质等知识,根据已知得出△BED∽△AEB是解题关键.

练习册系列答案
相关题目
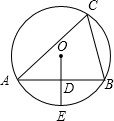 如图,⊙O是△ABC的内接圆,OD⊥AB于点D,交⊙O于点E,∠C=60°,如果⊙O的半径为4,则结论错误的是( )
如图,⊙O是△ABC的内接圆,OD⊥AB于点D,交⊙O于点E,∠C=60°,如果⊙O的半径为4,则结论错误的是( )| A、AD=DB | ||
| B、弧AE=弧EB | ||
| C、OD=2 | ||
D、AB=2
|
 如图,锐角△ABC中,PQRS是△ABC的内接矩形,且S△ABC=nS矩形PQRS,其中n为不小于3的自然数.求证:
如图,锐角△ABC中,PQRS是△ABC的内接矩形,且S△ABC=nS矩形PQRS,其中n为不小于3的自然数.求证: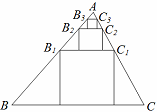 如图,在△ABC中,BC=3,S△ABC=3,B1C1所在四边形是△ABC的内接正方形,则B1C1的长为
如图,在△ABC中,BC=3,S△ABC=3,B1C1所在四边形是△ABC的内接正方形,则B1C1的长为 如图,四边形DEFG是△ABC的内接矩形,如果△ABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,则y关于x的函数关系式为
如图,四边形DEFG是△ABC的内接矩形,如果△ABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,则y关于x的函数关系式为 如图,△ABC中,已知AB=AC,△DEF是△ABC的内接正三角形,α=∠BDF,β=∠CED,γ=∠AFE,则用β、γ表示α的关系式是
如图,△ABC中,已知AB=AC,△DEF是△ABC的内接正三角形,α=∠BDF,β=∠CED,γ=∠AFE,则用β、γ表示α的关系式是