题目内容
图 1
1 是边长分别为4
是边长分别为4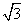 和2的两个等边三角形纸片ABC和ODE叠放在一起(C与O重合).
和2的两个等边三角形纸片ABC和ODE叠放在一起(C与O重合).
(1)操作:固定△ABC,将△0DE绕点C顺时针旋转30°后得到△ODE,连结AD、BE,CE的延长线交AB于F(图2);
探究:在图2中,线段BE与AD之间有怎样的大小关系?试证明你的结论.
(2)在(1)的条件下将的△ODE,在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△PQR,当点P与点F重合时停止运动(图3)
探究:设△PQR移动的时间为x秒,△PQR与△ABC重叠部分的面积为y,求y与x之间的函数解析式,并写出函数自变量x的取值范围.
(3)将图1中△0DE固定,把△ABC沿着OE方向平移,使顶点C落在OE的中点G处,设为△ABG,然后将△ABG绕点G顺时针旋转,边BG交边DE于点M,边AG交边DO于点N,设∠BGE=α(30°<α<90°);(图4)
 探究:在图4中,线段ON·EM的值是否随α的变化而变化?如果没有变化,请你
探究:在图4中,线段ON·EM的值是否随α的变化而变化?如果没有变化,请你
求出ON·EM的值,如果有变化,请你说明理由.
练习册系列答案
相关题目


 的自变量x的取值范围在数轴上表示为
的自变量x的取值范围在数轴上表示为
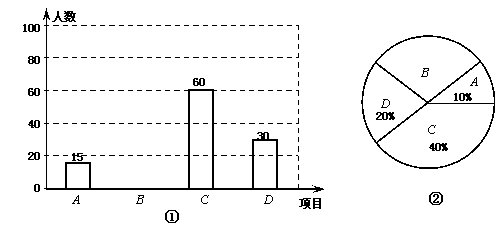 (3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
 k和b的值;
k和b的值;
 BAD=( ).
BAD=( ).
 的图象经过点(
的图象经过点( 1,-2),则k的值为( )
1,-2),则k的值为( ) C.1 D.-2
C.1 D.-2 ,然后从1、2、–1中选出一个作a的值,求出代数式的值.
,然后从1、2、–1中选出一个作a的值,求出代数式的值.